题目内容
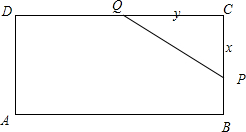
在矩形ABCD中，AB=5，BC=2，现截去一个角△PCQ，使P、Q分别落在边BC、CD上，且△PCQ的周长为8，设PC=x，CQ=y，则用x表示y的表达式为y=______．
如图
由题意可得0≤x≤2，由勾股定理可得PQ=
，
故△PCQ的周长=x+y+
=8，即
=8-x-y，
平方可得x2+y2=64+x2+y2-16x-16y+2xy，
整理可得32=8x+8y-xy，即（8-x）y=32-8x，
故y=
，（0≤x≤2）
故答案为：
，（0≤x≤2）
由题意可得0≤x≤2，由勾股定理可得PQ=
| x2+y2 |
故△PCQ的周长=x+y+
| x2+y2 |
| x2+y2 |
平方可得x2+y2=64+x2+y2-16x-16y+2xy，
整理可得32=8x+8y-xy，即（8-x）y=32-8x，
故y=
| 32-8x |
| 8-x |
故答案为：
| 32-8x |
| 8-x |
练习册系列答案
阅读快车系列答案
相关题目
的反函数
的图象与y轴交于点
（如图1所示），则方程
的根是
（ ）
________．
的反函数是_____________________。
那么