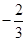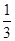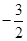题目内容
已知f(x)=x2-2x+1,g(x)是一次函数,且f[g(x)]=4x2,求g(x)的解析式.
设g(x)=ax+b(a≠0),
则f[g(x)]=(ax+b)2-2(ax+b)+1
=a2x2+(2ab-2a)x+b2-2b+1=4x2.
解得a=±2,b=1.
∴g(x)=2x+1或g(x)=-2x+1.
则f[g(x)]=(ax+b)2-2(ax+b)+1
=a2x2+(2ab-2a)x+b2-2b+1=4x2.
|
解得a=±2,b=1.
∴g(x)=2x+1或g(x)=-2x+1.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 的图象上一点
的图象上一点 及邻近一点
及邻近一点 ,则
,则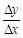 等于( )
等于( )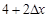

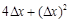
 ,则导函数
,则导函数 是( )
是( ) 的反函数为
的反函数为 ,则满足
,则满足 的x的集合是
的x的集合是 在
在 处的导数为1,则
处的导数为1,则 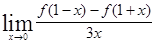 = ( )
= ( )