题目内容
如图,直三棱柱A1B1C1—ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(1)求![]() 与平面A1C1CA所成角的大小;
与平面A1C1CA所成角的大小;
(2)求二面角B—A1D—A的大小;
(3)点F是线段AC的中点,证明:EF⊥平面A1BD.
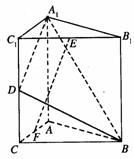
解:(1)连接A1C.∵A1B1C1-ABC为直三棱柱,∴CC1⊥底面ABC,∴CC1⊥BC.
∵AC⊥CB,∴BC⊥平面A1C1CA. ………………1分
∴![]() 为
为![]() 与平面A1C1CA所成角,
与平面A1C1CA所成角,
![]() .
.
∴![]() 与平面A1C1CA所成角为
与平面A1C1CA所成角为![]() . ………3分
. ………3分
(2)分别延长AC,A1D交于G. 过C作CM⊥A1G 于M,连结BM,
∵BC⊥平面ACC1A1,∴CM为BM在平面A1C1CA内的射影,
∴BM⊥A1G,∴∠CMB为二面角B—A1D—A的平面角, ………………………5分
平面A1C1CA中,C1C=CA=2,D为C1C的中点,
∴CG=2,DC=1 在直角三角形CDG中,![]() ,
,![]() . ……7分
. ……7分
即二面角B—A1D—A的大小为![]() . ……………………8分
. ……………………8分
(3)证明:∵A1B1C1—ABC为直三棱柱,∴B1C1//BC,
∵由(Ⅰ)BC⊥平面A1C1CA,∴B1C1⊥平面A1C1CA,
∵EF在平面A1C1CA内的射影为C1F,∵F为AC中点,
∴C1F⊥A1D,∴EF⊥A1D. ……………………11分
同理可证EF⊥BD,∴EF⊥平面A1BD. ……………………12分
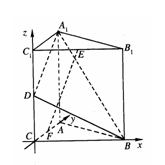
解法二:
(1)同解法一……………………3分
(2)∵A1B1C1—ABC为直三棱柱,C1C=CB=CA=2,
AC⊥CB,D、E分别为C1C、B1C1的中点.
建立如图所示的坐标系得:
C(0,0,0),B(2,0,0),A(0,2,0),
C1(0,0,2), B1(2,0,2), A1(0,2,2),
D(0,0,1), E(1,0,2). ………………6分
![]() ,设平面A1BD的法向量为
,设平面A1BD的法向量为![]()
![]() ,
,
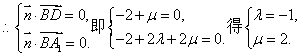
![]() . …………6分
. …………6分
平面ACC1A1的法向量为![]() =(1,0,0),
=(1,0,0),![]() . ………7分
. ………7分
即二面角B—A1D—A的大小为![]() . …………………8分
. …………………8分
(3)证明:∵F为AC的中点,∴F(0,1,0),![]() . ……10分
. ……10分
由(Ⅱ)知平面A1BD的一个法向量为![]() ,∴
,∴![]() //n . ……11分
//n . ……11分
EF⊥平面A1BD. ………………………………12分

 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,M,N分别为A1B,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,M,N分别为A1B,B1C1的中点. 如图,直三棱柱ABCA1B1C1的底面ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
如图,直三棱柱ABCA1B1C1的底面ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点. (2013•大兴区一模)如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.
(2013•大兴区一模)如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点. (2013•凉山州二模)如图,直三棱柱ABC-A1B1C1中,AB=AC,BC=2BB1,D为BC中点.
(2013•凉山州二模)如图,直三棱柱ABC-A1B1C1中,AB=AC,BC=2BB1,D为BC中点.