题目内容
7．已知tanθ=-3，θ∈（$\frac{3}{2}$π，2π），则3sinθ-cosθ的值为（ ）| A． | $\frac{4}{5}$$\sqrt{10}$ | B． | -$\frac{4}{5}$$\sqrt{10}$ | C． | -$\sqrt{10}$ | D． | $\frac{2}{5}$$\sqrt{10}$ |
分析 由tanθ的值，及θ的范围，利用同角三角函数间的基本关系求出cosθ与sinθ的值，代入原式计算即可得到结果．
解答 解：∵tanθ=-3，θ∈（$\frac{3}{2}$π，2π），
∴cosθ=$\sqrt{\frac{1}{1+ta{n}^{2}θ}}$=$\frac{\sqrt{10}}{10}$，sinθ=-$\sqrt{1-co{s}^{2}θ}$=-$\frac{3\sqrt{10}}{10}$，
则原式=3×（-$\frac{3\sqrt{10}}{10}$）-$\frac{\sqrt{10}}{10}$=-$\sqrt{10}$，
故选：C．
点评 此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
18．
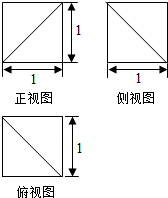某几何体的三视图如图所示，则该几何体的体积是（ ）
某几何体的三视图如图所示，则该几何体的体积是（ ）| A． | $\frac{5}{6}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{6}$ |
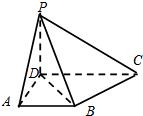如图，四棱锥P-ABCD中，底面ABCD为梯形，PD⊥底面ABCD，AB∥CD，AD⊥CD，AD=AB=1，BC=$\sqrt{2}$．