题目内容
(本题满分16分;第(1)小题5分,第(2)小题5分,第(3)小题6分)
设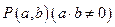 、
、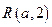 为坐标平面
为坐标平面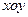 上的点,直线
上的点,直线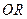 (
(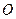 为坐标原点)与抛物线
为坐标原点)与抛物线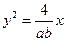 交于点
交于点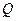 (异于
(异于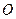 ).
).
(1) 若对任意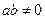
 ,点
,点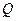 在抛物线
在抛物线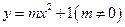 上,试问当
上,试问当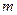 为何值时,点
为何值时,点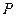 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程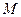 ;
;
(2) 若点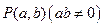 在椭圆
在椭圆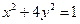 上,试问:点
上,试问:点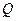 能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
(3) 对(1)中点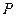 所在圆方程
所在圆方程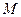 ,设
,设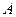 、
、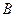 是圆
是圆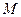 上两点,且满足
上两点,且满足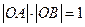 ,试问:是否存在一个定圆
,试问:是否存在一个定圆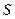 ,使直线
,使直线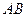 恒与圆
恒与圆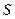 相切.
相切.
设
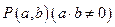 、
、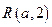 为坐标平面
为坐标平面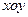 上的点,直线
上的点,直线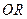 (
(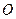 为坐标原点)与抛物线
为坐标原点)与抛物线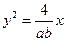 交于点
交于点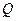 (异于
(异于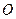 ).
).(1) 若对任意
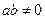
 ,点
,点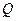 在抛物线
在抛物线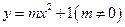 上,试问当
上,试问当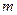 为何值时,点
为何值时,点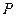 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程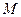 ;
;(2) 若点
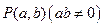 在椭圆
在椭圆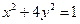 上,试问:点
上,试问:点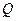 能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;(3) 对(1)中点
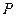 所在圆方程
所在圆方程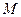 ,设
,设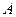 、
、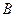 是圆
是圆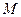 上两点,且满足
上两点,且满足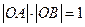 ,试问:是否存在一个定圆
,试问:是否存在一个定圆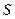 ,使直线
,使直线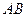 恒与圆
恒与圆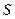 相切.
相切.(1)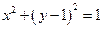 (2)
(2) (3)
(3)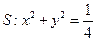
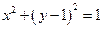 (2)
(2) (3)
(3)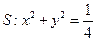
(1)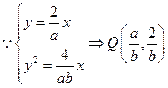 ,-----------------------------------------------------2分
,-----------------------------------------------------2分
代入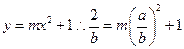
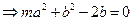 ---------------------------------- 4分
---------------------------------- 4分
当 时,点
时,点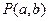 在圆
在圆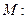
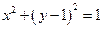 上-------------------------------------------5分
上-------------------------------------------5分
(2) 在椭圆
在椭圆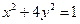 上,即
上,即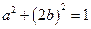
 可设
可设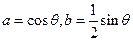 ------------------------------------------------------------------------7分
------------------------------------------------------------------------7分
又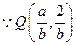 ,于是
,于是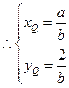
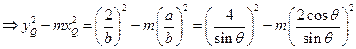
 (令
(令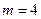 )
)
 点
点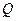 在双曲线
在双曲线 上--------------------------------------------------------------------10分
上--------------------------------------------------------------------10分
(3)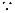 圆
圆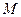 的方程为
的方程为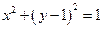
设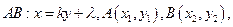 由
由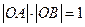
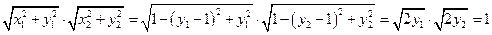
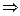
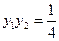 ---------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------- -12分
-12分
又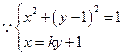
 ,
,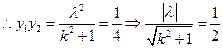 ------------14分
------------14分
又原点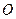 到直线
到直线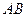 距离
距离
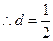 ,即原点
,即原点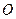 到直线
到直线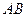 的距离恒为
的距离恒为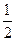
 直线
直线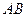 恒与圆
恒与圆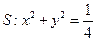 相切。-----------------------------------
相切。----------------------------------- ----------------------16分
----------------------16分
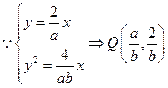 ,-----------------------------------------------------2分
,-----------------------------------------------------2分代入
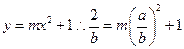
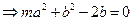 ---------------------------------- 4分
---------------------------------- 4分当
 时,点
时,点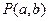 在圆
在圆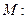
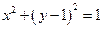 上-------------------------------------------5分
上-------------------------------------------5分(2)
 在椭圆
在椭圆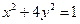 上,即
上,即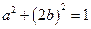
 可设
可设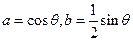 ------------------------------------------------------------------------7分
------------------------------------------------------------------------7分又
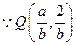 ,于是
,于是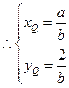
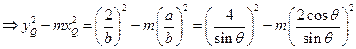
 (令
(令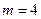 )
) 点
点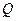 在双曲线
在双曲线 上--------------------------------------------------------------------10分
上--------------------------------------------------------------------10分(3)
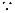 圆
圆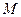 的方程为
的方程为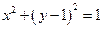
设
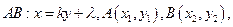 由
由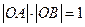
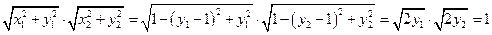
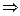
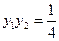 ---------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------- -12分
-12分又
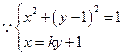
 ,
,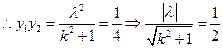 ------------14分
------------14分又原点
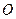 到直线
到直线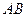 距离
距离
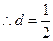 ,即原点
,即原点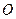 到直线
到直线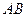 的距离恒为
的距离恒为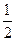
 直线
直线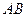 恒与圆
恒与圆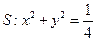 相切。-----------------------------------
相切。----------------------------------- ----------------------16分
----------------------16分
练习册系列答案
相关题目
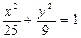 上一点,
上一点,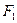 、
、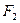 为左右焦点,若
为左右焦点,若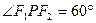
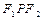 的面积;
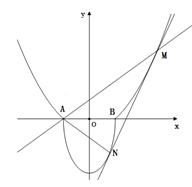
的面积;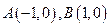 ,过曲线
,过曲线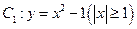 上一点
上一点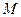 的切线
的切线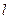 ,与曲线
,与曲线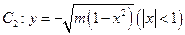 也相切于点
也相切于点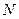 ,记点
,记点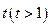 。
。
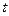 表示切线
表示切线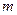 的值和点
的值和点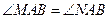 ?
?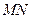 所在直线的方程。
所在直线的方程。 (
( 为参数)没有公共点,则实数m的取值范围是 。
为参数)没有公共点,则实数m的取值范围是 。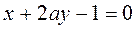 与直线
与直线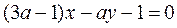 平行,求a的值.
平行,求a的值.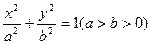 的焦点F(c, 0)的弦中最短弦长是 ( )
的焦点F(c, 0)的弦中最短弦长是 ( )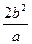
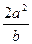
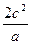
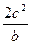
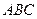 的重心
的重心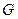 任作一直线分别交
任作一直线分别交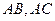 于
于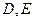 ,
,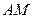 为中线
为中线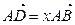 ,
,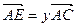 ,
,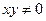 ,求
,求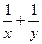 的值
的值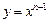 (
(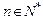 )在点
)在点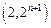 处的切线与
处的切线与 轴交点的横坐标为
轴交点的横坐标为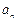 ,则
,则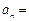 .
.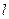 的斜率
的斜率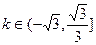 ,则此直线的倾斜角
,则此直线的倾斜角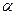 的取值范围为 ;
的取值范围为 ;