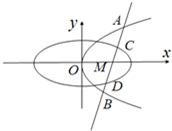
题目内容

已知椭圆C1：
x2
4
+
y2
3
=1和抛物线C2：y2=2px（p＞0），过点M（1，0）且倾斜角为
π
3
的直线与抛物线交于A、B，与椭圆交于C、D，当|AB|：|CD|=5：3时，求p的值．
设直线方程是
x=1+
1
2
t
y=
3
2
t
(t是参数)，分别代入椭圆、抛物线方程得：
5t2+4t-12=0（1）3t2-4pt-8p=0（2）
设A、B、C、D的参数分别为t1、t2、t3、t4，
则|AB|=|t1-t2|=
4
p2+6p
3
，|CD|=|t3-t4|=
16
5
，由|AB|：|CD|=5：3解得p=2．
练习册系列答案
相关题目
椭圆C1：
x2
a2
+
y2
b2
=1(a＞b＞0)与抛物线C2：x2=2py（p＞0）的一个交点为M．抛物线C2在点M处的切线过椭圆C1的右焦点F．
（1）若M(2，
2
5
5
)，求C1和C2的标准方程；
（II）若b=1，求p关于a的函数表达式p=f（a）．
双曲线x2-y2=a2截直线4x+5y=0的弦长为
41
，则此双曲线的实轴长为（　　）
A．3B．
3
2
C．
12
5
D．
6
5
椭圆C的中心在原点O，焦点在x轴，它的短轴长为2，过焦点与x轴垂直的直线与椭圆C相交于A，B两点且|AB|=1．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过定点N（1，0）的直线l交椭圆C于C、D两点，交y轴于点P，若
PC
=λ1
CN
，
PD
=λ2
DN
，求证：λ1+λ2为定值．
已知抛物线y2=8x与椭圆
x2
a2
+
y2
b2
=1有公共焦点F，且椭圆过点D（-
2
，
3
）．
（1）求椭圆方程；
（2）点A、B是椭圆的上下顶点，点C为右顶点，记过点A、B、C的圆为⊙M，过点D作⊙M的切线l，求直线l的方程；
（3）过点A作互相垂直的两条直线分别交椭圆于点P、Q，则直线PQ是否经过定点，若是，求出该点坐标，若不经过，说明理由．
设椭圆的中心为坐标原点O，焦点在x轴上，焦距为2，F为右焦点，B1为下顶点，B2为上顶点，S△B1FB2=1．
（I）求椭圆的方程；
（Ⅱ）若直线l同时满足下列三个条件：①与直线B1F平行；②与椭圆交于两个不同的点P、Q；③S△POQ=
2
3
，求直线l的方程．
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)经过点A（2，1），离心率为
2
2
．过点B（3，0）的直线l与椭圆C交于不同的两点M，N．
（Ⅰ）求椭圆C的方程；
（Ⅱ）求
BM
•
BN
的取值范围；
（Ⅲ）设直线AM和直线AN的斜率分别为kAM和kAN，求证：kAM+kAN为定值．
设双曲线C的中心在原点，焦点在x轴上，离心率为2，其一个顶点的坐标是(
1
3
，0)；又直线l：y=kx+1与双曲线C相交于不同的A、B两点．
（Ⅰ）求双曲线C的标准方程；
（Ⅱ）是否存在实数k，使得以线段AB为直径的圆过坐标的原点？若存在，求出k的值；若不存在，写出理由．
（文）已知椭圆
x2
36
+
y2
9
=1的一条弦的中点为P（4，2），求此弦所在直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网