题目内容
【题目】如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F 分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l. 
(Ⅰ)求证:直线l⊥平面PAC;
(Ⅱ)直线l上是否存在点Q,使直线PQ分别与平面AEF、直线EF所成的角互余?若存在,求出|AQ|的值;若不存在,请说明理由.
【答案】(Ⅰ)证明:∵E,F分别是PB,PC的中点,∴BC∥EF, 又EF平面EFA,BC不包含于平面EFA,
∴BC∥面EFA,
又BC面ABC,面EFA∩面ABC=l,
∴BC∥l,
又BC⊥AC,面PAC∩面ABC=AC,
面PAC⊥面ABC,∴BC⊥面PAC,
∴l⊥面PAC.
(Ⅱ)解:以C为坐标原点,CA为x轴,CB为y轴,
过C垂直于面ABC的直线为z轴,建立空间直角坐标系,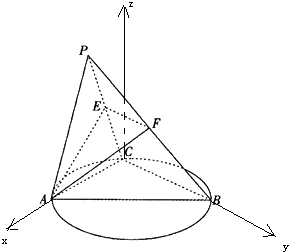
A(2,0,0),B(0,4,0),P(1,0, ![]() ),
),
E( ![]() ),F(
),F( ![]() ),
),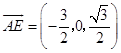 ,
, ![]() ,
,
设Q(2,y,0),面AEF的法向量为 ![]() ,
,
则 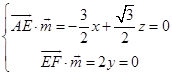 ,
,
取z= ![]() ,得
,得 ![]() ,
, ![]() ,
,
|cos< ![]() >|=
>|= 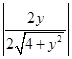 =
= 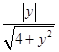 ,
,
|cos< ![]() >|=
>|= 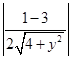 =
= ![]() ,
,
依题意,得|cos< ![]() >|=|cos<
>|=|cos< ![]() >|,
>|,
∴y=±1.
∴直线l上存在点Q,使直线PQ分别与平面AEF、直线EF所成的角互余,|AQ|=1.
【解析】(Ⅰ)利用三角形中位线定理推导出BC∥面EFA,从而得到BC∥l,再由已知条件推导出BC⊥面PAC,由此证明l⊥面PAC.(2)以C为坐标原点,CA为x轴,CB为y轴,过C垂直于面ABC的直线为z轴,建立空间直角坐标系,利用向量法求出直线l上存在点Q,使直线PQ分别与平面AEF、直线EF所成的角互余,|AQ|=1.

练习册系列答案
相关题目




