Question

【题目】定义在R上的奇函数f（x），当x≥0时，f（x）=，则关于x的函数F（x）=f（x）-的所有零点之和为______．

Answer 1

【答案】

【解析】

根据分段函数的解析式和奇函数的对称性作出函数在上的图象和的图象，利用数形结合的方法求解即可

∵当x≥0时，f（x）=；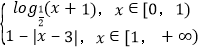

即x∈时，f（x）=

x∈[1，3]时，f（x）=x-2∈[-1，1]；

x∈（3，+∞）时，f（x）=4-x∈（-∞，-1）

画出x≥0时f（x）的图象，

再利用奇函数的对称性，画出x＜0时f（x）的图象，如图所示；

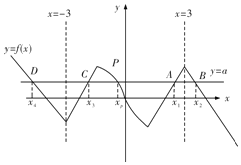
则直线，与y=f（x）的图象有5个交点，则方程f（x）-=0共五个实根，

最左边两根之和为-6，最右边两根之和为6，

∵x∈（-1，0）时，-x∈（0，1），∴f（-x）=

又f（-x）=-f（x），

∴f（x）=-=

∴中间的一个根满足

即1-x=，解得x=1-，

∴所有根的和为

故答案为：