题目内容
从1,2,3,4,5这五个数字中,先任意抽取一个,然后再从剩下的四个数字中再抽取一个,求下列事件的概率:(1)第一次抽到的是奇数;
(2)第一次抽到的是偶数;
(3)两次抽到的都是奇数;
(4)两次抽到的都是偶数;
(5)两次抽到的数字之和是偶数.
【答案】分析:(1)从1,2,3,4,5这五个数字中,任意抽取一个有5种不同抽法,而抽到的是奇数有3种不同的抽法,由古典概型公式得到结果.
(2)从1,2,3,4,5这五个数字中,任意抽取一个有5种不同抽法,而抽到的是偶数有2种不同的抽法,由古典概型公式得结果.
(3)从1,2,3,4,5这五个数字中,任意抽取两个数字有C52种不同抽法,而抽到的是奇数有C32种方法,由古典概型公式得结果.
(4)从1,2,3,4,5这五个数字中,任意抽取两个数字有C52种不同抽法,而抽到的是偶数有1种方法,由古典概型公式得结果.
(5)从1,2,3,4,5这五个数字中,任意抽取两个数字有C52种不同抽法,而抽到的数字之和是偶数有两种不同的情况.第一抽的是两个偶数,第二抽到的是两个奇数.
解答:解:(1)从1,2,3,4,5这五个数字中,
任意抽取一个有5种不同抽法,
而抽到的是奇数有3种不同的抽法,
由古典概型公式得P=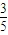 ,
,
(2)从1,2,3,4,5这五个数字中,
任意抽取一个有5种不同抽法,
而抽到的是偶数有2种不同的抽法,
由古典概型公式得P=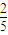 .
.
(3)从1,2,3,4,5这五个数字中,
任意抽取两个数字有C52种不同抽法,
而抽到的是奇数有C32种方法,
由古典概型公式得P=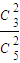 =
=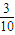 .
.
(4)从1,2,3,4,5这五个数字中,
任意抽取两个数字有C52种不同抽法,
而抽到的是偶数有1种方法,
由古典概型公式得P=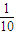 .
.
(5)从1,2,3,4,5这五个数字中,
任意抽取两个数字有C52种不同抽法,
而抽到的数字之和是偶数有两种不同的情况.第一抽的是两个偶数有1种方法,
第二抽到的是两个奇数有C32=3种方法.
由古典概型公式得P=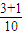 =
=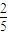 .
.
点评:解题时先要判断该概率模型是不是古典概型,再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数.最后根据古典概型公式得到结果.
(2)从1,2,3,4,5这五个数字中,任意抽取一个有5种不同抽法,而抽到的是偶数有2种不同的抽法,由古典概型公式得结果.
(3)从1,2,3,4,5这五个数字中,任意抽取两个数字有C52种不同抽法,而抽到的是奇数有C32种方法,由古典概型公式得结果.
(4)从1,2,3,4,5这五个数字中,任意抽取两个数字有C52种不同抽法,而抽到的是偶数有1种方法,由古典概型公式得结果.
(5)从1,2,3,4,5这五个数字中,任意抽取两个数字有C52种不同抽法,而抽到的数字之和是偶数有两种不同的情况.第一抽的是两个偶数,第二抽到的是两个奇数.
解答:解:(1)从1,2,3,4,5这五个数字中,
任意抽取一个有5种不同抽法,
而抽到的是奇数有3种不同的抽法,
由古典概型公式得P=
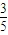 ,
,(2)从1,2,3,4,5这五个数字中,
任意抽取一个有5种不同抽法,
而抽到的是偶数有2种不同的抽法,
由古典概型公式得P=
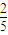 .
.(3)从1,2,3,4,5这五个数字中,
任意抽取两个数字有C52种不同抽法,
而抽到的是奇数有C32种方法,
由古典概型公式得P=
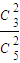 =
=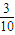 .
.(4)从1,2,3,4,5这五个数字中,
任意抽取两个数字有C52种不同抽法,
而抽到的是偶数有1种方法,
由古典概型公式得P=
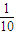 .
.(5)从1,2,3,4,5这五个数字中,
任意抽取两个数字有C52种不同抽法,
而抽到的数字之和是偶数有两种不同的情况.第一抽的是两个偶数有1种方法,
第二抽到的是两个奇数有C32=3种方法.
由古典概型公式得P=
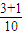 =
=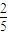 .
.点评:解题时先要判断该概率模型是不是古典概型,再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数.最后根据古典概型公式得到结果.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
从1,2,3,4,5,6,7,8,9中不放回地依次取2个数,事件A=“第一次取到的是奇数”,B=“第二次取到的是奇数”,则P(B|A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|