题目内容
如果函数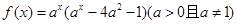 在区间
在区间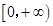 上是增函数,那么实数
上是增函数,那么实数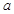 的取值范围是 .
的取值范围是 .
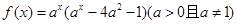 在区间
在区间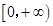 上是增函数,那么实数
上是增函数,那么实数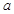 的取值范围是 .
的取值范围是 . 
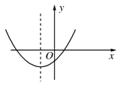
因为函数y=ax(ax-4a2-1)(a>0且a≠1)可以看作是关于ax的二次函数,
若a>1,则y=ax是增函数,原函数在区间[0,+∞)上是增函数,要求对称轴小于等于零,不符合舍去。
若0<a<1,则y=ax是减函数,原函数在区间[0,+∞)上是增函数,
则要求当t=ax(0<t<1)时,
y=t2-(3a2+1)t在t∈(0,1)上为减函数,要求对称轴大于等于1,可知a的范围为
若a>1,则y=ax是增函数,原函数在区间[0,+∞)上是增函数,要求对称轴小于等于零,不符合舍去。
若0<a<1,则y=ax是减函数,原函数在区间[0,+∞)上是增函数,
则要求当t=ax(0<t<1)时,
y=t2-(3a2+1)t在t∈(0,1)上为减函数,要求对称轴大于等于1,可知a的范围为


练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
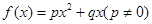 ,其导函数为
,其导函数为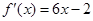 ,数列
,数列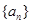 的前
的前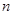 项和为
项和为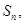 点
点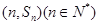 均在函数
均在函数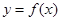 的图像上;.
的图像上;.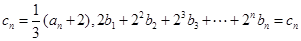 ,求数列
,求数列 的通项公式;
的通项公式;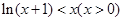 成立,
成立,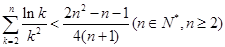
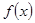 在
在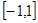 上是增函数,且
上是增函数,且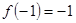 ,若
,若 对所有的
对所有的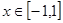 都成立,当
都成立,当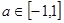 时,则
时,则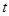 的取值范围是( )
的取值范围是( )
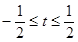


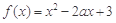 在区间
在区间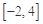 的值域为
的值域为 ,则实数
,则实数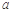 的取值范围为____________。
的取值范围为____________。  ,或
,或 ,且
,且 ,则
,则

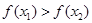
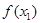 与
与 的大小不能确定
的大小不能确定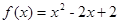 在区间
在区间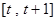
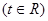 上的最小值记为
上的最小值记为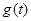

 的解集为
的解集为 ,求实数
,求实数 的取值范围;
的取值范围;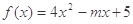 在区间
在区间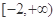 上是增函数,则
上是增函数,则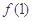 的取值范围是 .
的取值范围是 .