题目内容
【题目】经过函数性质的学习,我们知道:“函数![]() 的图象关于
的图象关于![]() 轴成轴对称图形”的充要条件是“
轴成轴对称图形”的充要条件是“![]() 为偶函数”.
为偶函数”.
(1)若![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() ,求
,求![]() 的解析式,并求不等式
的解析式,并求不等式![]() 的解集;
的解集;
(2)某数学学习小组针对上述结论进行探究,得到一个真命题:“函数![]() 的图象关于直线
的图象关于直线![]() 成轴对称图形”的充要条件是“
成轴对称图形”的充要条件是“![]() 为偶函数”.若函数
为偶函数”.若函数![]() 的图象关于直线
的图象关于直线![]() 对称,且当
对称,且当![]() 时,
时,![]() .
.
(i)求![]() 的解析式;
的解析式;
(ii)求不等式![]() 的解集.
的解集.
【答案】(1) ![]() 不等式的解集是
不等式的解集是![]() 或
或![]() .(2)
.(2) ![]()
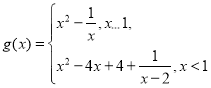 ,(ii)不等式的解集为
,(ii)不等式的解集为![]() .
.
【解析】
(1)根据函数对称性得出![]() 在
在![]() 上的解析式,再列出不等式得出不等式的解集;
上的解析式,再列出不等式得出不等式的解集;
(2)![]() 根据
根据![]() 是偶函数得出
是偶函数得出![]() 在
在![]() 上的解析式,(ii)根据单调性和对称性列不等式得出解集.
上的解析式,(ii)根据单调性和对称性列不等式得出解集.
(1)设![]() ,则
,则![]() ,则
,则![]() ,
,
又![]() 为偶函数,所以
为偶函数,所以![]() .
.
所以![]() .
.
因为![]() 为偶函数,且
为偶函数,且![]() 在
在![]() ,
,![]() 上是减函数,
上是减函数,
所以![]() 等价于
等价于![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() .
.
所以不等式的解集是![]() 或
或![]() .
.
(2)![]() 因为
因为![]() 的图象关于直线
的图象关于直线![]() 对称,所以
对称,所以![]() 为偶函数,
为偶函数,
所以![]() ,即
,即![]() 对任意
对任意![]() 恒成立.
恒成立.
又当![]() 时,
时,![]() ,
,
所以![]() .
.
所以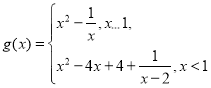
![]() 任取
任取![]() ,
,![]() ,
,![]() ,且
,且![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,又
,又![]() ,
,![]() ,
,
所以![]() ,即
,即![]() .
.
所以函数![]() 在
在![]() ,
,![]() 上是增函数,
上是增函数,
又因为函数![]() 的图象关于直线
的图象关于直线![]() 对称,
对称,
所以![]() 等价于
等价于![]() ,
,
即![]() ,解得
,解得![]() .
.
所以不等式的解集为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某公司需要对所生产的![]() 三种产品进行检测,三种产品数量(单位:件)如下表所示:
三种产品进行检测,三种产品数量(单位:件)如下表所示:
产品 | A | B | C |
数量(件) | 180 | 270 | 90 |
采用分层抽样的方法从以上产品中共抽取6件.
(1)求分别抽取三种产品的件数;
(2)将抽取的6件产品按种类![]() 编号,分别记为
编号,分别记为![]() ,现从这6件产品中随机抽取2件.
,现从这6件产品中随机抽取2件.
(ⅰ)用所给编号列出所有可能的结果;
(ⅱ)求这两件产品来自不同种类的概率.