题目内容
.已知数列{an}满足a1=1,a2=r(r>0),数列{bn}是公比为q的等比数列(q>0),bn=anan+1,cn=a2n-1+a2n,求cn。
Cn=(1+r)qn-1
解析试题分析:∵bn+1=bnq, ∴an+1an+2=anan+1q ∴an+2=anq,即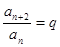
由a1=1,a3=q,a5=q2,……,知奇数项构成一个等比数列,故a2n-1=qn-1
由a2=r,a4=rq,a6=rq2,……,知偶数项也构成一个等比数,故a2n=rqn-1
∴Cn=(1+r)qn-1
考点:本题主要考查等比数列的概念、通项公式及等比数列的性质。
点评: 灵活运用等比数列的性质,结合通项公式,达到解题目的。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知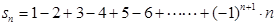 ,则
,则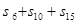 等于( )
等于( )
A.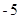 | B.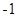 | C. | D. |
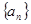 的首项为
的首项为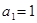 ,其前
,其前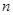 项和为
项和为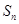 ,且对任意正整数
,且对任意正整数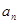 、
、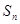 成等差数列.
成等差数列.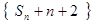 成等比数列;
成等比数列;  的相邻两项
的相邻两项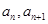 是关于
是关于 的方程
的方程 的两根,且
的两根,且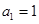
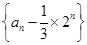 是等比数列;
是等比数列; 项和
项和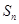 ;
;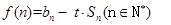 若
若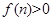 对任意的
对任意的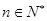 都成立,求
都成立,求 的取值范围。
的取值范围。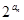 +2n,求数列{bn}的前n项和Tn.
+2n,求数列{bn}的前n项和Tn. 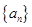 的各项均为正数,且
的各项均为正数,且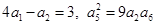 . (1)求数列
. (1)求数列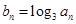 ,求数列
,求数列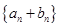 的前
的前 项和
项和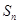 .
.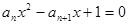 ,
,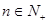 有两根
有两根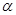 和
和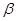 ,且满足
,且满足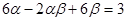 ,
,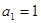
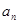 表示
表示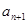 ;
; 是等比数列;
是等比数列;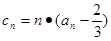 ,
, 为
为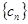 的前n项和,证明
的前n项和,证明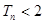 ,(
,(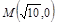 作直线
作直线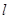 交曲线
交曲线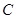 :
: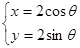 (
(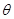 为参数)于
为参数)于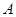 、
、 两点,若
两点,若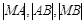 成等比数列,求直线
成等比数列,求直线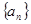 中,
中,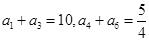 ,求
,求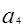 及其前5项的和
及其前5项的和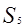 .
.