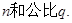题目内容
(本小题满分13分)
已知数列 的相邻两项
的相邻两项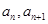 是关于
是关于 的方程
的方程 的两根,且
的两根,且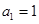
(1)求证:数列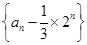 是等比数列;
是等比数列;
(2)求数列 的前
的前 项和
项和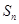 ;
;
(3)设函数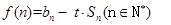 若
若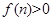 对任意的
对任意的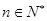 都成立,求
都成立,求 的取值范围。
的取值范围。
(1)∵an+an+1=2n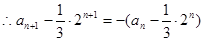
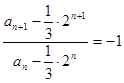
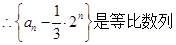 。
。
(2)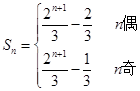 ;(3)t<1。
;(3)t<1。
解析试题分析:(1)∵an+an+1=2n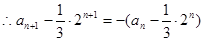
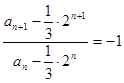
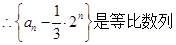
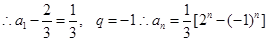 (3分)
(3分)
(2)Sn=a1+a2+……+an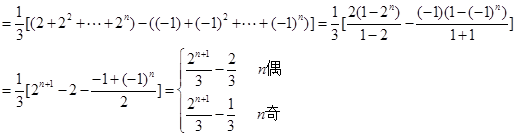 (6分)
(6分)
(3)bn=an·an+1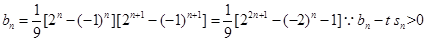
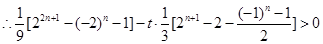 ∴当n为奇数时
∴当n为奇数时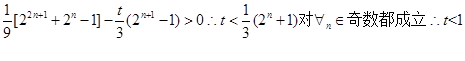 (9分)
(9分)
当n为偶数时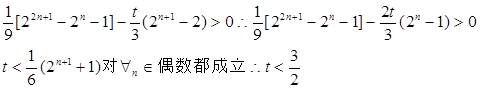 (12分)
(12分)
综上所述,t的取值范围为t<1 (13分)
考点:等比数列的定义;数列通项公式的求法;数列前n项和的求法。
点评:若已知递推公式为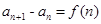 的形式求通项公式常用累加法。
的形式求通项公式常用累加法。
注:①若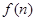 是关于n的一次函数,累加后可转化为等差数列求和;
是关于n的一次函数,累加后可转化为等差数列求和;
②若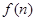 是关于n的二次函数,累加后可分组求和;
是关于n的二次函数,累加后可分组求和;
③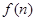 是关于n的指数函数,累加后可转化为等比数列求和;
是关于n的指数函数,累加后可转化为等比数列求和;
④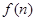 是关于n的分式函数,累加后可裂项求和。
是关于n的分式函数,累加后可裂项求和。

练习册系列答案
相关题目
数列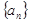 的通项公式
的通项公式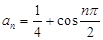
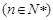 ,其前n项和为Sn,则S2012等于( )
,其前n项和为Sn,则S2012等于( )
| A.1006 | B.2012 | C.503 | D.0 |
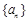 的前n项和为
的前n项和为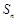 ,
, ,且
,且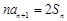 ,数列
,数列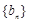 满足
满足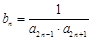 ,数列
,数列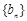 的前n项和为
的前n项和为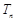 (其中
(其中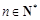 ).
).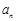 和
和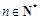 ,不等式
,不等式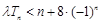 恒成立,求实数
恒成立,求实数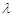 的取值范围
的取值范围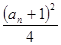
 是一个公差为
是一个公差为 的等差数列,它的前10项和
的等差数列,它的前10项和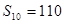 且
且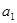 ,
,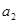 ,
,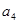 成等比数列.(Ⅰ)证明
成等比数列.(Ⅰ)证明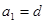 ; (Ⅱ)求公差
; (Ⅱ)求公差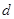 的值和数列
的值和数列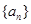 是公比大于1的等比数列,
是公比大于1的等比数列,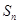 为数列
为数列 项和.已知
项和.已知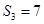 ,且
,且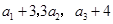 构成等差数列.
构成等差数列.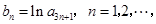 求数列
求数列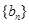 的前
的前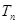 .
.  前n项和
前n项和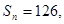 求
求