题目内容
10.在约束条件$\left\{\begin{array}{l}y≥x\\ y≤2x\\ x+y≤1\end{array}\right.$下,目标函数z=x+2y的最大值为$\frac{5}{3}$.分析 先画出满足条件的平面区域,将z=x+2y转化为y=-$\frac{1}{2}$x+$\frac{z}{2}$,通过图象读出即可.
解答 解:画出满足条件的平面区域,如图示: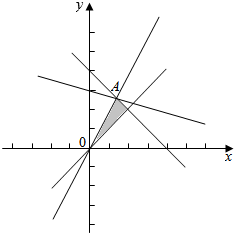 ,
,
由$\left\{\begin{array}{l}{y=2x}\\{x+y=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{2}{3}}\end{array}\right.$,
由z=x+2y得:y=-$\frac{1}{2}$x+$\frac{z}{2}$,
显然,直线y=-$\frac{1}{2}$x+$\frac{z}{2}$过A($\frac{1}{3}$,$\frac{2}{3}$)时,z最大,
∴z最大值=$\frac{5}{3}$,
故答案为:$\frac{5}{3}$.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
1.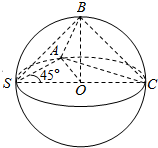 已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为( )
已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为( )
 已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为( )
已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{5\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
18.若正数x,y满足$\frac{1}{x}$+$\frac{9}{y}$=1,则xy的( )
| A. | 最大值为6 | B. | 最小值为6 | C. | 最大值为36 | D. | 最小值为36 |