题目内容
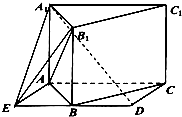
如图,直三棱柱ABC-A1B1C1的底面ABC位于矩形AEDC中,B点为ED的中点,AC=AA1=2AE=2.
(1)求异面直线AB1与A1D所成角的余弦值;
(2)求平面A1B1E与平面AEDC所成二面角大小的余弦值.
(1)求异面直线AB1与A1D所成角的余弦值;
(2)求平面A1B1E与平面AEDC所成二面角大小的余弦值.

(Ⅰ)以A为原点,建立空间直角坐标系A-xyz如图所示,则A1(0,0,2),B1(1,1,0),B(1,1,2),D(1,2,0),E(1,1,0)
从而
=(1,1,2),
=(1,2,-2)
∴cos<
,
>=-
又由两异面直线夹角的范围是(0,
]
∴异面直线AB1与A1D所成角的余弦值为
(II)设
=(x,y,z)为平面A1B1E的一个法向量
∵
=(1,0,-2),
=
=(1,1,0)
由
,即
令z=1,得平面A1B1E的一个法向量
=(2,-2,1)
又∵
=
=(0,0,2)是平面AEDC的一个法向量
由cos<
,
>=
=
得
平面A1B1E与平面AEDC所成二面角的余弦值为

从而
| AB1 |
| A1D |
∴cos<
| AB1 |
| A1D |
| ||
| 18 |
又由两异面直线夹角的范围是(0,
| π |
| 2 |
∴异面直线AB1与A1D所成角的余弦值为
| ||
| 18 |
(II)设
| n |
∵
| A1E |
| A1B1 |
| AB |
由
|
|
令z=1,得平面A1B1E的一个法向量
| n |
又∵
| m |
| AA1 |
由cos<
| m |
| n |
| 2 |
| 2×3 |
| 1 |
| 3 |
平面A1B1E与平面AEDC所成二面角的余弦值为
| 1 |
| 3 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





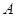 、
、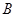 、
、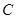 是圆
是圆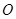 上的三点,
上的三点,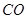 的延长线与线段
的延长线与线段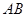 交于圆内一点
交于圆内一点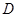 ,若
,若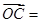
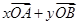 ,则 ( )
,则 ( )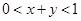
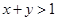
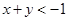
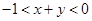
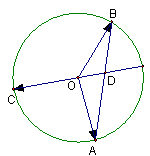
 ,
, ,
, ,若
,若 三点共线,则实数
三点共线,则实数 的值为 _ .
的值为 _ .