题目内容
（2011•潍坊二模）已知非零向量
、
满足|
|=
|
|，若函数f(x)=
x3+|
|x2+2
•
x+1在R上有极值，则＜
，
＞的取值范围是（ ）
| a |
| b |
| a |
| 3 |
| b |
| 1 |
| 3 |
| a |
| a |
| b |
| a |
| b |
分析：根据三次函数在R上有极值，可知方程f′（x）=0有两个不等的实数根，从而判别式大于0，结合条件|
|=
|
|，可求＜
，
＞的取值范围．
| a |
| 3 |
| b |
| a |
| b |
解答：解：∵f(x)=
x3+|
|x2+2
•
x+1
∴f′(x)=x2+2|
|x+2
•
令f′（x）=0
∵函数f(x)=
x3+|
|x2+2
•
x+1在R上有极值
∴方程f′（x）=0有两个不等的实数根
∴△=4|
|2 -8
•
＞ 0
∵|
|=
|
|
∴12|
|2-8
|
|2cos＜
，
＞＞0
∴cos＜
，
＞＜
∵0≤＜
，
＞≤π
∴
＜＜
，
＞≤π
∴＜
，
＞的取值范围是(
，π]
故选D．
| 1 |
| 3 |
| a |
| a |
| b |
∴f′(x)=x2+2|
| a |
| a |
| b |
令f′（x）=0
∵函数f(x)=
| 1 |
| 3 |
| a |
| a |
| b |
∴方程f′（x）=0有两个不等的实数根
∴△=4|
| a |
| a |
| b |
∵|
| a |
| 3 |
| b |
∴12|
| b |
| 3 |
| b |
| a |
| b |
∴cos＜
| a |
| b |
| ||
| 2 |
∵0≤＜
| a |
| b |
∴
| π |
| 6 |
| a |
| b |
∴＜
| a |
| b |
| π |
| 6 |
故选D．
点评：本题以函数极值为载体，考查导数知识的运用，考查向量的数量积，解题的关键是转化为方程f′（x）=0有两个不等的实数根．
练习册系列答案
相关题目
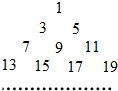（2011•潍坊二模）已知数列an=2n-1（n∈N*），把数列{an}的各项排成如图所示的三角形数阵，记（m，n）表示该数阵中第m行中从左到右的第n个数，则S（10，6）对应于数阵中的数是
（2011•潍坊二模）运行如图的程序框图，当输入m=-4时的输出结果为n，若变量x，y满足