题目内容
 (2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足
(2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足
|
5
5
.分析:分析:先根据程序框图得到n的值,再画出约束条件
,的可行域,再求出可行域中各角点的坐标,将各点坐标代入目标函数的解析式,分析后易得目标函数z=2x+y的最大值.
|
解答: 解:由程序框图运行的结果得:n=1,
解:由程序框图运行的结果得:n=1,
由约束条件
,得如图所示的三角形区域,
三个顶点坐标为A(2,1),B(1,2),C(0,1)
将三个代入得z的值分别为10,8,2
直线z=2x+y过点A (2,1)时,z取得最大值为5;
故答案为:5.
 解:由程序框图运行的结果得:n=1,
解:由程序框图运行的结果得:n=1,由约束条件
|
三个顶点坐标为A(2,1),B(1,2),C(0,1)
将三个代入得z的值分别为10,8,2
直线z=2x+y过点A (2,1)时,z取得最大值为5;
故答案为:5.
点评:点评:在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.

练习册系列答案
相关题目
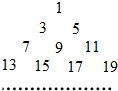 (2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是
(2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是