题目内容
(2011•潍坊二模)已知
=(cos?x,sin?x),
=(cos?x,2
cos?x-sin?x),?>0,函数f(x)=
•
+|
|,x1,x2是集合M={x|f(x)=1}中任意两个元素,且|x1-x2|的最小值为
.
(1)求?的值.
(2)在△ABC中,a,b,c分别是A,B,C的对边.f(A)=2,c=2,S△ABC=
,求a的值.
| m |
| n |
| 3 |
| m |
| n |
| m |
| π |
| 2 |
(1)求?的值.
(2)在△ABC中,a,b,c分别是A,B,C的对边.f(A)=2,c=2,S△ABC=
| ||
| 2 |
分析:(1)由向量的知识可对式子化简,由题意易得周期,进而可得?的值;
(2)代入解析式可得C,由余弦定理和面积公式联合可得关于ab的方程组,解之即可.
(2)代入解析式可得C,由余弦定理和面积公式联合可得关于ab的方程组,解之即可.
解答:解:(1)由题意可知:f(x)=
•
+|
|
=cos2?x+2
sin?xcos?x-sin2?x+1
=cos2?x+
sin2?x+1
=2sin(2?x+
)+1,
又x1,x2是集合M={x|f(x)=1}中任意两个元素,且|x1-x2|的最小值为
,
所以函数f(x)的半周期为
,即
=
×2,解得?=1
(2)由(1)可知f(x)=2sin(2x+
)+1,进而可得2sin(2C+
)+1=2,
化简得sin(2C+
)=
,解得C=
,
由余弦定理可得22=a2+b2-2abcos
=(a+b)2-3ab,
由S△ABC=
absinC=
ab=
,可得ab=2,
综合上面两式可得a+b=
,ab=2,故ab为方程x2-
x+2=0的根,
解得a=
,或
| m |
| n |
| m |
=cos2?x+2
| 3 |
=cos2?x+
| 3 |
=2sin(2?x+
| π |
| 6 |
又x1,x2是集合M={x|f(x)=1}中任意两个元素,且|x1-x2|的最小值为
| π |
| 2 |
所以函数f(x)的半周期为
| π |
| 2 |
| 2π |
| 2? |
| π |
| 2 |
(2)由(1)可知f(x)=2sin(2x+
| π |
| 6 |
| π |
| 6 |
化简得sin(2C+
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
由余弦定理可得22=a2+b2-2abcos
| π |
| 3 |
由S△ABC=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
综合上面两式可得a+b=
| 10 |
| 10 |
解得a=
| ||||
| 2 |
| ||||
| 2 |
点评:本题考查向量的数量积,以及解三角形的知识,属中档题.

练习册系列答案
相关题目
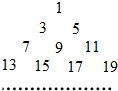 (2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是
(2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 (2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足
(2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足