题目内容
（2011•潍坊二模）设p：
＜0，q：0＜x＜m，若p是q成立的充分不必要条件，则m的取值范围是
| x | x-2 |
（2，+∞）
（2，+∞）
．分析：将条件关系转化为集合的包含关系；据集合的包含关系得到集合的端点的大小关系，列出不等式即可求出m的范围．
解答：解：解不等式
＜0可得：0＜x＜2，
因为p是q成立的充分不必要条件，
所以集合{x|0＜x＜2}是集合{x|0＜x＜m}的真子集
∴m＞2
故答案为：（2，+∞）
| x |
| x-2 |
因为p是q成立的充分不必要条件，
所以集合{x|0＜x＜2}是集合{x|0＜x＜m}的真子集
∴m＞2
故答案为：（2，+∞）
点评：本题考查利用集合关系来判断条件关系．当A?B时，A是B的充分不必要条件是解决问题的关键，属基础题．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
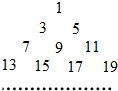（2011•潍坊二模）已知数列an=2n-1（n∈N*），把数列{an}的各项排成如图所示的三角形数阵，记（m，n）表示该数阵中第m行中从左到右的第n个数，则S（10，6）对应于数阵中的数是
（2011•潍坊二模）运行如图的程序框图，当输入m=-4时的输出结果为n，若变量x，y满足