题目内容
【题目】
等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD 所在的平面和平面ABEF互相垂直.
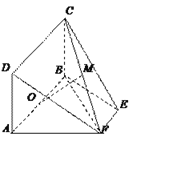
(1)求证:AF⊥平面CBF;
(2)设FC的中点为M,求证:OM∥平面DAF;
(3)求三棱锥C-BEF的体积.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)要证线与面垂直,需先证明直线![]() 垂直于平面内的两条相交直线,因为矩形
垂直于平面内的两条相交直线,因为矩形![]() 所在的平面和平面
所在的平面和平面![]() 互相垂直,所以
互相垂直,所以![]() 垂直于平面
垂直于平面![]() ,从而
,从而![]() 垂直于
垂直于![]() ,依题意,
,依题意,![]() 垂直于
垂直于![]() ,从而命题得证;(2)取
,从而命题得证;(2)取![]() 的中点为
的中点为![]() ,由三角形中位线定理,
,由三角形中位线定理,![]() 平行
平行![]() 且等于
且等于![]() 的一半,而
的一半,而![]() 也是如此,从而
也是如此,从而![]() 平行且等于
平行且等于![]() ,四边形
,四边形![]() 为平行四边形,所以
为平行四边形,所以![]() 平行于
平行于![]() ,由线面平行的判定定理即可得证
,由线面平行的判定定理即可得证![]() 平行于平面
平行于平面![]() ;(3)先计算底面三角形
;(3)先计算底面三角形![]() 的面积,在等腰梯形
的面积,在等腰梯形![]() 中,可得此三角形的高为
中,可得此三角形的高为![]() ,底
,底![]() 为1,再计算三棱锥
为1,再计算三棱锥![]() 的高,即为
的高,即为![]() ,最后由三棱锥体积计算公式计算即可.
,最后由三棱锥体积计算公式计算即可.
试题解析:(1) ∵平面ABCD⊥平面ABEF,CB⊥AB,
平面ABCD∩平面ABEF=AB,∴CB⊥平面ABEF,
∵AF平面ABEF,∴AF⊥CB.
又∵AF⊥BF,BF∩BC=B,BF,BC平面CBF.
∴AF⊥平面CBF.
(2) 设DF的中点为N,则MN∥CD,MN=CD,
AO∥CD,AO=CD,则MN∥AO,MN=AO,
∴四边形MNAO是平行四边形,∴OM∥AN.
又AN平面DAF,OM平面DAF,∴OM∥平面DAF.
(3) 过点E作EH⊥AB于H,则∠EBH=60°,
所以EH=![]() ,EF=AB-2HB=1,故S△BEF=×1×
,EF=AB-2HB=1,故S△BEF=×1×![]() =
=![]() ,VC-BEF=×S△BEF×BC=
,VC-BEF=×S△BEF×BC=![]() .
.

【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为![]() .
.
(1)请将上述列联表补充完整;
(2)并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(3)已知在被调查的学生中有5名来自甲班,其中3名喜欢游泳,现从这5名学生中随机抽取2人,求恰好有1人喜欢游泳的概率.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: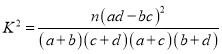 ,其中
,其中![]() )
)
【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如下图:记成绩不低于70分者为“成绩优良”.
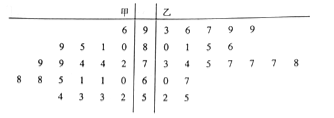
(1)分别计算甲、乙两班20个样本中,化学分数前十的平均分,并大致判断哪种教学方式的教学效果更佳;
(2)由以上统计数据填写下面![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为“成绩优良与教学方式有关”?
的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附:![]()
独立性检验临界值表:
|
|
|
|
|
|
|
|
|
|
【题目】某城市一汽车出租公司为了调查A,B两种车型的出租情况,现随机抽取了这两种车型各100辆,分别统计了每辆车某个星期内的出租天数,统计数据如下表:
A车型 B车型
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 | 车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
(Ⅰ)从出租天数为3天的汽车(仅限A,B两种车型)中随机抽取一辆,估计这辆汽车恰好是A型车的概率;
(Ⅱ)根据这个星期的统计数据,估计该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4天的概率;
(Ⅲ)
(ⅰ)试写出A,B两种车型的出租天数的分布列及数学期望;
(ⅱ)如果两种车辆每辆车每天出租获得的利润相同,该公司需要从A,B两种车型中购买一辆(注:两种车型的采购价格相当),请你根据所学的统计知识,建议应该购买哪一种车型,并说明你的理由.