Question

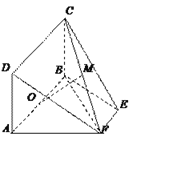
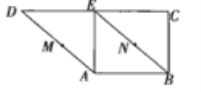
【题目】如图，在直角梯形ABCD中，AB∥DC，AE⊥DC，BE∥AD.M、N分别是AD、BE上的点，且AM=BN，将三角形ADE沿AE折起，则下列说法正确的是 (填上所有正确说法的序号).

①不论D折至何位置(不在平面ABC内)都有MN∥平面DEC；

②不论D折至何位置都有MN⊥AE；

③不论D折至何位置(不在平面ABC内)都有MN∥AB；

④在折起过程中,一定存在某个位置，使EC⊥AD.

Answer 1

【答案】①②④

【解析】连接MN，交AE于点P，则MP∥DE，NP∥AB，∵AB∥CD，∴NP∥CD.

对于①，由题意可得平面MNP∥平面DEC，∴MN∥平面DEC，故①正确；

对于②，∵AE⊥MP，AE⊥NP，MP∩NP=P，∴AE⊥平面MNP，∴AE⊥MN，故②正确；

对于③，∵NP∥AB，∴不论D折至何位置(不在平面ABC内)都不可能有MN∥AB，故③不正确；

对于④，由题意知EC⊥AE，故在折起的过程中，当EC⊥DE时，EC⊥平面ADE，∴EC⊥AD，故④正确.