题目内容
已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式;
(2)若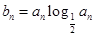 ,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值.
,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值.
(1)an=2n. (2)n的最小值为5.
解析试题分析:(1)解 设等比数列{an}的首项为a1,公比为q.依题意,有2(a3+2)=a2+a4,代入a2+a3+a4=28,可得a3=8,∴a2+a4=20,所以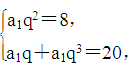 解之得
解之得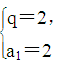 或
或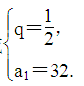 又∵数列{an}单调递增,所以q=2,a1=2,∴数列{an}的通项公式为an=2n.(2)因为bn=2nlog
又∵数列{an}单调递增,所以q=2,a1=2,∴数列{an}的通项公式为an=2n.(2)因为bn=2nlog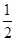 2n=-n·2n,所以Sn=-(1×2+2×22+…+n·2n),2Sn=-[1×22+2×23+…+(n-1)·2n+n·2n+1],两式相减,得
2n=-n·2n,所以Sn=-(1×2+2×22+…+n·2n),2Sn=-[1×22+2×23+…+(n-1)·2n+n·2n+1],两式相减,得
Sn=2+22+23+…+2n-n·2n+1=2n+1-2-n·2n+1.要使Sn+n·2n+1>50,即2n+1-2>50,即2n+1≥52.
易知:当n≤4时,2n+1≤25=32<52;当n≥5时,2n+1≥26=64>52.故使Sn+n·2n+1>50成立的正整数n的最小值为5.
考点:等比数列的通项公式
点评:主要是考查了等比数列的通项公式和求和的运用,属于基础题。

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 满足
满足 ,
, (
( 且
且 ).
). ;
; ,记数列
,记数列 的前
的前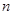 项和为
项和为 ,若
,若 恒为一个与
恒为一个与 ,试求常数
,试求常数 和
和 }的前n项和为
}的前n项和为 ,
, ,
, .
. ,证明:数列
,证明:数列 是等比数列;
是等比数列; 的前
的前 项和
项和 ;
; ,
, .求不超过
.求不超过 的最大整数的值。
的最大整数的值。 中,
中, ,
, (
( 是常数,
是常数, ),且
),且 成公比不为
成公比不为 的等比数列.
的等比数列.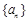 的前n项和为
的前n项和为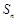 ,
, ,且
,且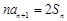 ,数列
,数列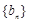 满足
满足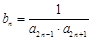 ,数列
,数列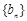 的前n项和为
的前n项和为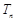 (其中
(其中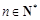 ).
).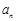 和
和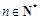 ,不等式
,不等式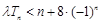 恒成立,求实数
恒成立,求实数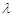 的取值范围
的取值范围 的首项为
的首项为 ,前
,前 项和为
项和为 ,且
,且 是
是 与
与 的等差中项
的等差中项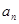 }中,
}中,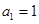 ,
,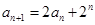 ,设
,设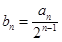 ,
,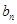 }是等差数列;
}是等差数列;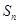 ;
;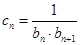 ,证明:
,证明: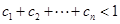
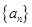 中,
中,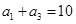 ,
,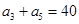 .设
.设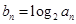 .
. 的通项公式;
的通项公式;  ,
,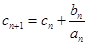 ,求证:
,求证: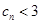 ;
;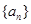 是公比大于1的等比数列,
是公比大于1的等比数列,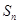 为数列
为数列 项和.已知
项和.已知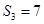 ,且
,且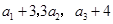 构成等差数列.
构成等差数列.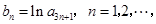 求数列
求数列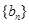 的前
的前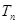 .
.