题目内容
11.如图,已知A,B,C是直线m上的三点,且|AB|=|BC|=6,⊙O切直线m于点A,又过B,C作异于直线m的两切线,切点分别为D,E,设两切线交于点P.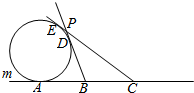
(1)求点P的轨迹E的方程;
(2)证明:已知S是轨迹E上异于A1,A2(轨迹E顶点)的一点,直线A1S,A2S分别交直线l:x=t(t为常数)于不同两点M,N,点Q在直线l上,若Q为线段MN的中点,则直线SQ与轨迹E有且只有一个公共点S.
分析 (1)设过B、C异于l的两切线分别切⊙O于D、E两点,两切线交于点P.由切线的性质,结合椭圆定义知,点P的轨迹是以B、C为两焦点的椭圆,建立坐标系,可求得动点P的轨迹方程;
(2)设S(x0,y0)(x0≠±2),求出A1S,A2S的方程,可得M,N的坐标,进而可得Q的坐标,求出SQ的方程,代入椭圆方程,求出△=0,即可得出结论.
解答 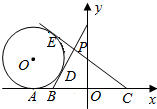 解:(1)设过B、C异于l的两切线分别切⊙O于D、E两点,两切线交于点P.
解:(1)设过B、C异于l的两切线分别切⊙O于D、E两点,两切线交于点P.
由切线的性质知:|BA|=|BD|,|PD|=|PE|,|CA|=|CE|,
故|PB|+|PC|=|BD|+|PD|+|PC|=|BA|+|PE|+|PC|=|BA|+|CE|=|AB|+|CA|=6+12=18>6=|BC|,
故由椭圆定义知,点P的轨迹是以B、C为两焦点的椭圆
以l所在的直线为x轴,以BC的中点为原点,建立坐标系,可求得动点P的轨迹方程为$\frac{{x}^{2}}{81}+\frac{{y}^{2}}{72}$=1(y≠0);
(2)证明:设S(x0,y0)(x0≠±9),
lA1S:y=$\frac{{y}_{0}}{{x}_{0}+9}$(x+9);lA2S:y=$\frac{{y}_{0}}{{x}_{0}-9}$(x-9),
∴M(t,$\frac{{y}_{0}(t+9)}{{x}_{0}+9}$),N(t,$\frac{{y}_{0}(t-9)}{{x}_{0}-9}$),
设MN的中点为Q(t,y1),则x1=t,y1=$\frac{{y}_{0}({x}_{0}t-9)}{{{x}_{0}}^{2}-81}$=-$\frac{-8({x}_{0}t-9)}{9{y}_{0}}$
∴Q(t,-$\frac{-8({x}_{0}t-9)}{9{y}_{0}}$),
∴kSQ=$\frac{{y}_{1}-{y}_{0}}{t-{x}_{0}}$=-$\frac{8{x}_{0}}{9{y}_{0}}$,
∴SQ的方程为y=-$\frac{8{x}_{0}}{9{y}_{0}}$(x-x0)+y0,即y=-$\frac{8{x}_{0}}{9{y}_{0}}$x+$\frac{8}{{y}_{0}}$
代入椭圆方程,消去y可得$\frac{8}{9{{y}_{0}}^{2}}$x2-$\frac{8{x}_{0}}{3{{y}_{0}}^{2}}$x+$\frac{8}{{{y}_{0}}^{2}}$-1=0,
∴△=(-$\frac{8{x}_{0}}{3{{y}_{0}}^{2}}$)2-4•$\frac{8}{9{{y}_{0}}^{2}}$•($\frac{8}{{{y}_{0}}^{2}}$-1)=0,
∴直线SQ与椭圆E有且只有一个公共点S.
点评 本题考查轨迹方程,考查椭圆的定义,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

| A. | (0,+∞) | B. | (1,+∞) | C. | (0,1) | D. | (0,1)∪(1,+∞) |
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 74 | 76 | 72 | 70 | 78 |
| A. | 80 | B. | 90 | C. | 86 | D. | 70 |