题目内容
11．P是直角△ABC所在平面外一点，若PA⊥平面ABC，PA=AB=AC，则平面PBC和平面ABC夹角的正切值是（ ）| A． | 1 | B． | $\sqrt{2}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | 2$\sqrt{2}$ |
分析 过点A作BC边上的高AD交BC于点D，连结PD．则∠PDA即为平面PBC和平面ABC夹角的平面角，利用勾股定理及三角形面积的不同计算方法即得结论．
解答 
解：过点A作BC边上的高AD交BC于点D，连结PD．
根据题意可得∠PDA即为平面PBC和平面ABC夹角的平面角，
设PA=AB=AC=a，则BC=$\sqrt{A{C}^{2}+A{B}^{2}}$=$\sqrt{2}$a，
∵$\frac{1}{2}$AD•BC=$\frac{1}{2}$AB•AC，
∴AD=$\frac{AB•AC}{BC}$=$\frac{\sqrt{2}}{2}$a，
∴tan∠PDA=$\frac{PA}{AD}$=$\frac{a}{\frac{\sqrt{2}a}{2}}$=$\sqrt{2}$，
故选：B．
点评 本题考查求二面角的三角函数值，涉及到勾股定理、三角形的面积计算公式等知识，注意解题方法的积累，属于中档题．
练习册系列答案
相关题目
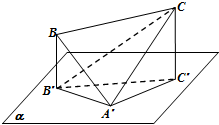如图，已知边长为2的正△A′BC，顶点A′在平面α内，顶点B，C在平面α外的同一侧，点B′，C′分别为B，C在平面α上的投影，设|BB′|≤|CC′|，直线CB′与平面A′CC′所成的角为φ．若△A′B′C′是以∠A′为直角的直角三角形，则tanφ的范围为$[{\frac{{\sqrt{2}}}{2}，\frac{{\sqrt{3}}}{2}}）$．
如图，已知点A（-2，0），点P是⊙B：（x-2）2+y2=36上任意一点，线段AP的垂直平分线交BP于点Q，点Q的轨迹记为曲线C．
如图，在正三棱柱ABC-A1B1C1中，点D在边BC上，AD⊥C1D．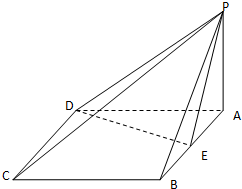
如图，四棱锥P-ABCD的底面ABCD是菱形，∠BCD=60°，PA⊥面ABCD，E是AB的中点．