题目内容
若x,y满足不等式组
且z=2x+4y的最小值为-6,则k的值为
|
0
0
.分析:由目标函数z=2x+4y的最小值是-6,我们可以画出满足条件
的可行域,根据目标函数的解析式形式,分析取得最优解的点的坐标,然后根据分析列出一个含参数k的方程,解之即可得到k的取值.
|
解答: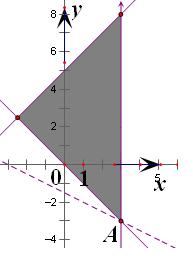 解:画出x,y满足的可行域
解:画出x,y满足的可行域
如下图:
由于目标函数z=2x+4y的最小值是-6,
可得直线x=3与直线-6=2x+4y的交点A(3,-3),
使目标函数z=2x+4y取得最小值,
将x=3,y=-3代入x+y-k=0得:
k=0,
故答案为:0.
 解:画出x,y满足的可行域
解:画出x,y满足的可行域
|
由于目标函数z=2x+4y的最小值是-6,
可得直线x=3与直线-6=2x+4y的交点A(3,-3),
使目标函数z=2x+4y取得最小值,
将x=3,y=-3代入x+y-k=0得:
k=0,
故答案为:0.
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.借助于平面区域特性,用几何方法处理代数问题,体现了数形结合思想、化归思想.线性规划中的最优解,通常是利用平移直线法确定.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
若x、y满足不等式组
,则x<
y的概率是( )
|
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|