题目内容
在一个盒子中,放有大小相同的红、白、黄三个小球,现从中任意摸出一球,若是红球记1分,白球记2分,黄球记3分.现从这个盒子中有放回地先后摸出两球,所得分数分别记为 、
、 ,设
,设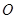 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为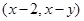 ,记
,记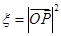 .
.
(1)求随机变量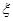 =5的概率;
=5的概率;
(2)求随机变量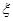 的分布列和数学期望.
的分布列和数学期望.
(1)
(2)随机变量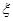 的分布列为:
的分布列为: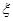



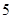

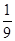

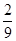
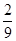
因此,数学
解析试题分析:解(Ⅰ) 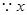 、
、 可能的取值为
可能的取值为 、
、 、
、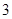 ,
,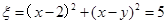 ,
,
且当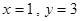 或
或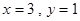 时,
时, ,又有放回摸两球的所有情况有
,又有放回摸两球的所有情况有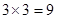 种,
种, . 6分
. 6分
(Ⅱ) 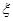 的所有取值为
的所有取值为 .
. 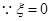 时,只有
时,只有 这一种情况.
这一种情况.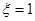 时,有
时,有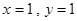 或
或 或
或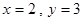 或
或 四种情况,
四种情况,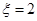 时,有
时,有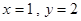 或
或 两种情况.
两种情况. 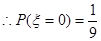 ,
, ,
, , 8分
, 8分
则随机变量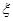 的分布列为:
的分布列为: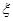



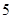

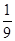

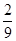
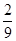
因此,数学 . 12分
. 12分
考点:古典概型
点评:主要四考查了古典概型概率的运用,以及分布列的求解属于中档题。

练习册系列答案
相关题目
某工厂有甲、乙两个生产小组,每个小组各有四名工人,某天该厂每位工人的生产情况如下表.
| | 员工号 | 1 | 2 | 3 | 4 |
| 甲组 | 件数 | 9 | 11 | 1l | 9 |
| | 员工号 | 1 | 2 | 3 | 4 |
| 乙组 | 件数 | 9 | 8 | 10 | 9 |
(2)求乙组员工生产件数的平均数和方差;
(3)分别从甲、乙两组中随机选取一名员工的生产件数,求这两名员工的生产总件数为19的概率.
(注:方差
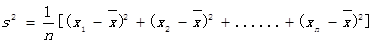 ,其中
,其中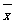 为x1,x2, ,xn的平均数)
为x1,x2, ,xn的平均数) 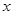 表示第
表示第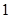 枚骰子出现的点数,
枚骰子出现的点数, 表示第
表示第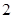 枚骰子出现的点数.
枚骰子出现的点数. 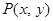 在直线
在直线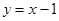 上的概率;
上的概率; 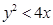 的概率.
的概率. 位学生,每次活动均需该系
位学生,每次活动均需该系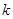 位学生参加(
位学生参加(
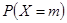 取得最大值的整数
取得最大值的整数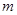 .
. ,乙每次击中目标的概率为
,乙每次击中目标的概率为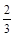
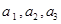 ,女生2名,记为
,女生2名,记为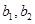 ,现从中任选2名学生去参加校数学竞赛
,现从中任选2名学生去参加校数学竞赛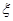 的概率密度函数
的概率密度函数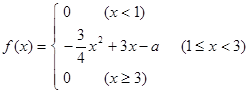 ,
, 的值,并画出
的值,并画出
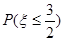 .
.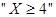 的概率。
的概率。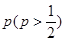 ,且各局胜负相互独立.已知
,且各局胜负相互独立.已知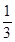 .
.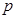 的值;
的值; 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量