题目内容
口袋中有5个大小相同的小球,其中1个小球标有数字“3”,2个小球标有数字“2”,2个小球标有数字“1”,每次从中任取一个小球,取后不放回,连续抽取两次。
(I)求两次取出的小球所标数字不同的概率;
(II)记两次取出的小球所标数字之和为X,求事件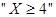 的概率。
的概率。
(I)(II)
解析试题分析:由题意可知,取法有(1a,1b),(1b,1a),(1a,2a),(1a,2b),(1b,2a),(1b,2b),(1a,3),(1b,3),(2a,1a),(2a,1b),(2b,1a),(2b,1b),(2a,3),
(2b,3),(2a,2b),(2b,2a),(3,1a),(3,1b),(3,2a),(3,2b),所有取法共10种
(I)两次取出的小球所标数字不同的取法有(1a,2a),(1a,2b),(1b,2a),(1b,2b),(1a,3),(1b,3),(2a,1a),(2a,1b),(2b,1a),(2b,1b),(2a,3),
(2b,3), (3,1a),(3,1b),(3,2a),(3,2b),共16种,所以两次取出的小球所标数字不同的概率为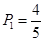 .
.
(II)两次取出的小球所标数字之和大于等于4的有(1a,3),(1b,3), (2a,3),
(2b,3),(2a,2b),(2b,2a),(3,1a),(3,1b),(3,2a),(3,2b),共10种,所以概率为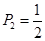 .
.
考点:本小题主要考查古典概型概率的求解.
点评:求解古典概型概率,主要是将基本事件一一列出来,所列的基本事件必须是等可能的.

某大学高等数学老师这学期分别用 两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
(Ⅰ)依茎叶图判断哪个班的平均分高?
(Ⅱ)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率;
(Ⅲ)学校规定:成绩不低于85分的为优秀,请填写下面的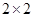 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
| | 甲班 | 乙班 | 合计 |
| 优秀 | | | |
| 不优秀 | | | |
| 合计 | | | |
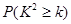 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
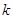 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
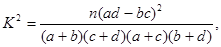 其中
其中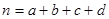 )
) 哈尔滨市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的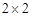 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为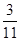 。
。
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:
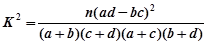 。
。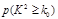 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
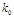 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
 、
、 ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为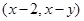 ,记
,记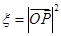 .
.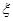 =5的概率;
=5的概率; ,乙队每人答对的概率都是
,乙队每人答对的概率都是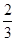 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用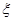 表示甲队总得分.
表示甲队总得分.