题目内容
已知a，b为正实数．
(1)求证：
≥a＋b；
(2)利用(1)的结论求函数y＝
(0<x<1)的最小值．
(1)求证：
≥a＋b；(2)利用(1)的结论求函数y＝
(0<x<1)的最小值．（1）见解析（2）1
(1)证明：方法一：∵a>0，b>0，
∴(a＋b)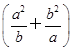
＝a2＋b2＋
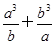≥a2＋b2＋2ab＝(a＋b)2.
∴≥a＋b，当且仅当a＝b时等号成立．
方法二：－(a＋b)
＝
，
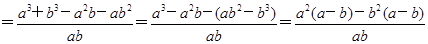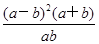又∵a>0，b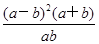>0，∴≥0，
当且仅当a＝b时等号成立．∴≥a＋b.
方法三：∵a>0，b>0，∴a2＋b2≥2ab.
∴a＋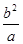
≥2b，b＋
≥2a，∴(a＋b)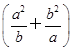＋≥2a＋2b.
∴≥a＋b.(当且仅当a＝b时取等号)．
(2)∵0<x<1，∴1－x>0，
由(1)的结论，函数y＝≥(1－x)＋x＝1.
当且仅当1－x＝x，即x＝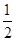
时等号成立．
∴函数y＝ (0<x<1)的最小值为1.
∴(a＋b)
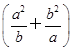＝a2＋b2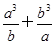＋≥a2＋b2＋2ab＝(a＋b)2.∴
≥a＋b，当且仅当a＝b时等号成立．方法二：
－(a＋b) 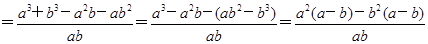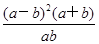＝，又∵a>0，b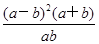>0，∴
≥0，当且仅当a＝b时等号成立．∴
≥a＋b.方法三：∵a>0，b>0，∴a2＋b2≥2ab.
∴a＋
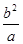≥2b，b＋≥2a，∴(a＋b)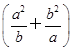＋≥2a＋2b.∴
≥a＋b.(当且仅当a＝b时取等号)．(2)∵0<x<1，∴1－x>0，
由(1)的结论，函数y＝
≥(1－x)＋x＝1.当且仅当1－x＝x，即x＝
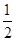时等号成立．∴函数y＝
(0<x<1)的最小值为1.
练习册系列答案
相关题目
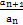,n∈N+.
·
.
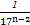＋abc≥2
.
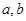满足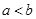
，则下列不等式中一定成立的是( )
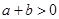
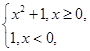则满足不等式f(1-x2)>f(2x)的x的取值范围是 .
的解集为 ．
(
+
)
