题目内容
【题目】设![]() 、
、![]() 是两个不同的平面,点
是两个不同的平面,点![]() 、
、![]() ,
,![]() 、
、![]() ,下列命题中正确的是( )
,下列命题中正确的是( )
A.若![]() ,
,![]() ,则
,则![]() ,
,![]()
B.若![]() ,
,![]() ,则
,则![]() ,
,![]()
C.若![]() ,
,![]() ,
,![]() ,则
,则![]() 、
、![]() ,
,![]()
D.若![]() ,
,![]() ,则
,则![]()
【答案】C
【解析】
利用四边形![]() 为等腰梯形且
为等腰梯形且![]() 判断A选项的正误;利用面面平行的性质定理结合平行四边形的性质可判断B选项的正误;利用面面、线面垂直的性质定理可判断C选项的正误;根据条件直接判断
判断A选项的正误;利用面面平行的性质定理结合平行四边形的性质可判断B选项的正误;利用面面、线面垂直的性质定理可判断C选项的正误;根据条件直接判断![]() 与
与![]() 的位置关系可判断D选项的正误.综合可得出结论.
的位置关系可判断D选项的正误.综合可得出结论.
对于A选项,若四边形![]() 为等腰梯形且
为等腰梯形且![]() ,则
,则![]() 与
与![]() 为梯形的两腰,不平行,A选项错误;
为梯形的两腰,不平行,A选项错误;
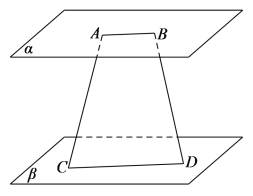
对于B选项,若![]() ,
,![]() ,则平面
,则平面![]() ,平面
,平面![]() ,
,
由面面平行的性质定理可得![]() ,所以,四边形
,所以,四边形![]() 为平行四边形,
为平行四边形,
则![]() ,但两条对角线长不一定相等,即
,但两条对角线长不一定相等,即![]() 不一定成立,B选项错误;
不一定成立,B选项错误;
对于C选项,设![]() ,如下图所示,过点
,如下图所示,过点![]() 在平面
在平面![]() 内作
内作![]() ,垂足为点
,垂足为点![]() ,
,
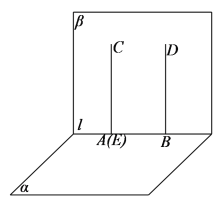
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,而过点
,而过点![]() 作平面
作平面![]() 的垂线,有且只有一条,且
的垂线,有且只有一条,且![]() ,则点
,则点![]() 与点
与点![]() 重合,
重合,
即![]() ,同理可得
,同理可得![]() ,
,![]() ,
,![]() ,C选项正确;
,C选项正确;
对于D选项,![]() ,
,![]() ,由于
,由于![]() 与
与![]() 的位置关系不确定,
的位置关系不确定,
则![]() 与
与![]() 平行、相交或异面,D选项错误.
平行、相交或异面,D选项错误.
故选:C.

【题目】某客户准备在家中安装一套净水系统,该系统为二级过滤,使用寿命为十年如图所示两个二级过滤器采用并联安装,再与一级过滤器串联安装.
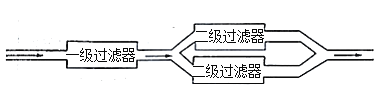
其中每一级过滤都由核心部件滤芯来实现在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立).若客户在安装净水系统的同时购买滤芯,则一级滤芯每个160元,二级滤芯每个80元.若客户在使用过程中单独购买滤芯则一级滤芯每个400元,二级滤芯每个200元.现需决策安装净水系统的同时购买滤芯的数量,为此参考了根据100套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中表1是根据100个一级过滤器更换的滤芯个数制成的频数分布表,图2是根据200个二级过滤器更换的滤芯个数制成的条形图.
表1:一级滤芯更换频数分布表
一级滤芯更换的个数 | 8 | 9 |
频数 | 60 | 40 |
图2:二级滤芯更换频数条形图
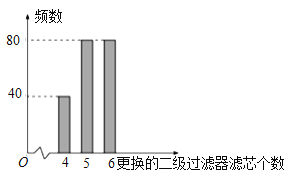
以100个一级过滤器更换滤芯的频率代替1个一级过滤器更换滤芯发生的概率,以200个二级过滤器更换滤芯的频率代替1个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() 的值.
的值.