题目内容
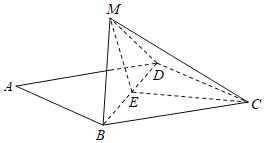
【题目】已知菱形ABCD中,∠BAD=60°,AC与BD相交于点O.将△ABD沿BD折起,使顶点A至点M,在折起的过程中,下列结论正确的是( )
A.BD⊥CM
B.存在一个位置,使△CDM为等边三角形
C.DM与BC不可能垂直
D.直线DM与平面BCD所成的角的最大值为60°
【答案】ABD
【解析】
画出图形,利用直线与直线的位置关系,直线与平面的位置关系判断选项的正误即可.
对A,菱形![]() 中,
中,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .将
.将![]() 沿
沿![]() 折起,使顶点
折起,使顶点![]() 至点
至点![]() ,如图:取
,如图:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,可知
,可知![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,可知
,可知![]() ,故A正确;
,故A正确;
对B,由题意可知![]() ,三棱锥是正四面体时,
,三棱锥是正四面体时,![]() 为等边三角形,故B正确;
为等边三角形,故B正确;
对C,三棱锥是正四面体时,![]() 与
与![]() 垂直,故C不正确;
垂直,故C不正确;
对D,平面![]() 与平面
与平面![]() 垂直时,直线
垂直时,直线![]() 与平面
与平面![]() 所成的角的最大值为
所成的角的最大值为![]() ,故D正确.
,故D正确.
故选:ABD.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖. 按文理科用分层抽样的方法抽取
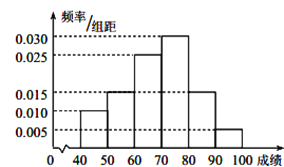
)的同学获奖. 按文理科用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).
(I)在答题卡上填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?
文科生 | 理科生 | 合计 | |
获奖 |
| ||
不获奖 | |||
合计 |
|
(II)将上述调査所得的频率视为概率,现从该校参与竞赛的学生中,任意抽取![]() 名学生,记“获奖”学生人数为
名学生,记“获奖”学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
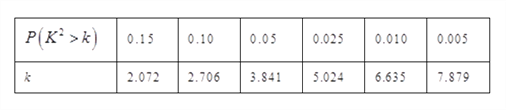
附表及公式:,其中
![]() .
.