题目内容
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为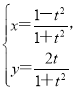 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求C的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)求C上的点到![]() 距离的最大值.
距离的最大值.
【答案】(1)C的普通方程为![]() .
.![]() 的直角坐标方程为
的直角坐标方程为![]() (2)3
(2)3
【解析】
(1)把曲线C的参数方程平方相加可得普通方程,把x=ρcosθ,y=ρsinθ代入ρcosθ![]() ρsinθ+4=0,可得直线l的直角坐标方程;
ρsinθ+4=0,可得直线l的直角坐标方程;
(2)设出椭圆上动点的坐标(参数形式),再由点到直线的距离公式写出距离,利用三角函数求最值.
(1)由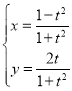 (t为参数),因为
(t为参数),因为![]() ,且
,且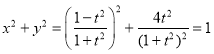 ,
,
所以C的普通方程为![]() .
.
由ρcosθ![]() ρsinθ+4=0,得x
ρsinθ+4=0,得x![]() y+4=0.
y+4=0.
即直线l的直角坐标方程为得x![]() y+4=0;
y+4=0;
(2)由(1)可设C的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).
).
则P到直线得x![]() y+4=0的距离为:
y+4=0的距离为:
C上的点到![]() 的距离为
的距离为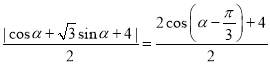 .
.
当![]() 时,
时,![]() 取得最大值6,故C上的点到
取得最大值6,故C上的点到![]() 距离的最大值为3.
距离的最大值为3.

【题目】眼保健操是一种眼睛的保健体操,主要是通过按摩眼部穴位,调整眼及头部的血液循环,调节肌肉,改善眼的疲劳,达到预防近视等眼部疾病的目的.某学校为了调查推广眼保健操对改善学生视力的效果,在应届高三的全体800名学生中随机抽取了100名学生进行视力检查,并得到如图的频率分布直方图.

(1)若直方图中后三组的频数成等差数列,试估计全年级视力在5.0以上的人数;
(2)为了研究学生的视力与眼保健操是否有关系,对年级不做眼保健操和坚持做眼保健操的学生进行了调查,得到下表中数据,根据表中的数据,能否在犯错的概率不超过0.005的前提下认为视力与眼保健操有关系?
是否做操 是否近视 | 不做操 | 做操 |
近视 | 44 | 32 |
不近视 | 6 | 18 |
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【题目】某工厂生产某种型号的电视机零配件,为了预测今年![]() 月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度
月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度![]() 月份至
月份至![]() 月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价
月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的
(单位:千件)之间的![]() 组数据如下表所示:
组数据如下表所示:
月份 |
|
|
|
|
|
|
销售单价 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
(1)根据1至![]() 月份的数据,求
月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(2)结合(1)中的线性回归方程,假设该型号电视机零配件的生产成本为每件![]() 元,那么工厂如何制定
元,那么工厂如何制定![]() 月份的销售单价,才能使该月利润达到最大(计算结果精确到
月份的销售单价,才能使该月利润达到最大(计算结果精确到![]() )?
)?
参考公式:回归直线方程![]() ,其中
,其中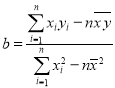 .
.
参考数据:![]() .
.
【题目】某市房产中心数据研究显示,2018年该市新建住宅销售均价如下表.3月至7月房价上涨过快,为抑制房价过快上涨,政府从8月份开始出台了相关限购政策,10月份开始房价得到了很好的抑制.
均价(万元/ | 0.95 | 0.98 | 1.11 | 1.12 | 1.20 | 1.22 | 1.32 | 1.34 | 1.16 | 1.06 |
月份 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
(Ⅰ)请建立3月至7月线性回归模型(保留小数点后3位),并预测若政府不宏观调控,12月份该市新建住宅销售均价;
(Ⅱ)试用相关系数说明3月至7月各月均价![]() (万元/
(万元/![]() )与月份
)与月份![]() 之间可用线性回归模型(保留小数点后2位)
之间可用线性回归模型(保留小数点后2位)
参考数据:![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
回归方程斜率和截距最小二乘法估计公式 ;
;
相关系数 .
.