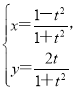题目内容
【题目】如图,在四面体![]() 中,
中,![]() ,
,![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,点
,点![]() 是
是![]() 的中点,求二面角
的中点,求二面角![]() 的大小.
的大小.
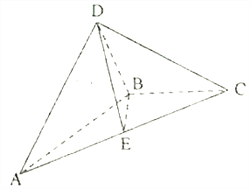
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】分析:(Ⅰ)由勾股定理可得![]() , 则
, 则![]() ,
,![]() ,进一步可得
,进一步可得![]() , 则
, 则![]() .
.
(Ⅱ)结合(Ⅰ)的结论和几何关系,以B为原点,建立空间直角坐标系![]() ,则平面BDE的法向量为
,则平面BDE的法向量为![]() ,且
,且![]() 是平面CBD的一个法向量.结合空间向量计算可得二面角
是平面CBD的一个法向量.结合空间向量计算可得二面角![]() 的大小为
的大小为![]() .
.
详解:(Ⅰ)由已知得![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
(Ⅱ)由(Ⅰ)知,AB与平面BCD所成的角为![]() ,即
,即![]() ,
,
设BD=2,则BC=2,在![]() 中,AB=4,
中,AB=4,
由(Ⅰ)中![]() ,得平面ABC⊥平面ABD,在平面ABD内,过点B作
,得平面ABC⊥平面ABD,在平面ABD内,过点B作![]() ,则
,则![]() 平面ABC,以B为原点,建立空间直角坐标系
平面ABC,以B为原点,建立空间直角坐标系![]() ,
,
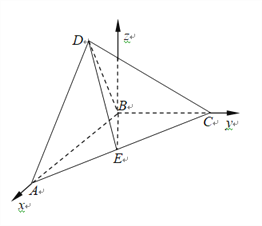
则![]() ,
,![]() ,
,![]() ,
,
![]() ,由
,由![]() ,
,
![]() ,
,
得![]() ,
,
∴![]() ,
,![]() ,
,
设平面BDE的法向量为![]() ,
,
则 ,取
,取![]() ,解得
,解得![]() ,
,
∴![]() 是平面BDE的一个法向量,
是平面BDE的一个法向量,
又![]() 是平面CBD的一个法向量.
是平面CBD的一个法向量.
设二面角![]() 的大小为
的大小为![]() ,易知
,易知![]() 为锐角,
为锐角,
则![]() ,
,
∴![]() ,即二面角
,即二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目