题目内容
已知椭圆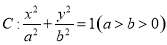 的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆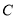 的标准方程;
的标准方程;
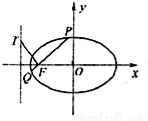
(2)设 为椭圆
为椭圆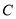 的左焦点,
的左焦点,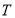 为左准线
为左准线 上任意一点,过
上任意一点,过 作
作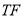 的垂线交椭圆
的垂线交椭圆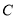 于点
于点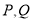 ,当
,当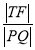 最小时,求点
最小时,求点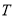 的坐标.
的坐标.
练习册系列答案
相关题目
题目内容
已知椭圆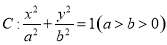 的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.

(1)求椭圆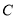 的标准方程;
的标准方程;
(2)设 为椭圆
为椭圆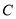 的左焦点,
的左焦点,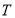 为左准线
为左准线 上任意一点,过
上任意一点,过 作
作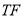 的垂线交椭圆
的垂线交椭圆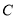 于点
于点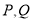 ,当
,当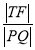 最小时,求点
最小时,求点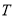 的坐标.
的坐标.