题目内容
(本小题满分14分)函数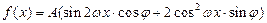
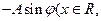
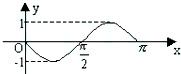
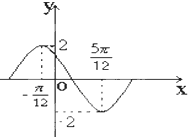
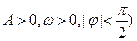 的图象在y轴右侧的第一个最高点(即函数取得最大值的点)为
的图象在y轴右侧的第一个最高点(即函数取得最大值的点)为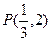 ,在原点右侧与x轴的第一个交点为Q(
,在原点右侧与x轴的第一个交点为Q(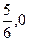 ). 求:(1)函数
). 求:(1)函数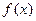 的表达式; (2)函数
的表达式; (2)函数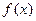 在区间
在区间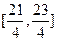 上的对称轴的方程.
上的对称轴的方程.
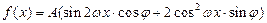
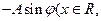
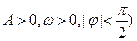 的图象在y轴右侧的第一个最高点(即函数取得最大值的点)为
的图象在y轴右侧的第一个最高点(即函数取得最大值的点)为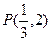 ,在原点右侧与x轴的第一个交点为Q(
,在原点右侧与x轴的第一个交点为Q(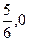 ). 求:(1)函数
). 求:(1)函数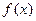 的表达式; (2)函数
的表达式; (2)函数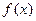 在区间
在区间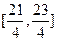 上的对称轴的方程.
上的对称轴的方程.:(1)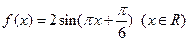 (2)
(2)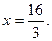
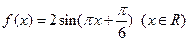 (2)
(2)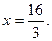
:(1)由题意可知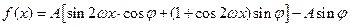


将点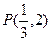 代入
代入 得:
得: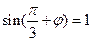 ,因为
,因为 , 所以
, 所以 ,
, 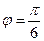 .
.
即函数的表达式为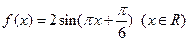
(2)由 ,解得:
,解得: 令
令
由于 所以函数
所以函数 上的对称轴的方程为
上的对称轴的方程为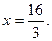
点评:本小题主要考查三角函数的基本公式、三角恒等变换、三角函数的图象和性质等基本知识,以及推理和运算能力。 三角函数的化简通常用到降幂、切化弦、和角差角公式的逆运算。
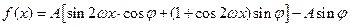


将点
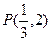 代入
代入 得:
得: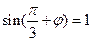 ,因为
,因为 , 所以
, 所以 ,
, 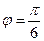 .
.即函数的表达式为
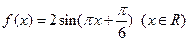
(2)由
 ,解得:
,解得: 令
令
由于
 所以函数
所以函数 上的对称轴的方程为
上的对称轴的方程为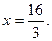
点评:本小题主要考查三角函数的基本公式、三角恒等变换、三角函数的图象和性质等基本知识,以及推理和运算能力。 三角函数的化简通常用到降幂、切化弦、和角差角公式的逆运算。

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 的最大值为3,
的最大值为3, 的图像的相邻两对称轴间的距离为2,在Y轴上的截距为2.
的图像的相邻两对称轴间的距离为2,在Y轴上的截距为2.  为其前n项和,求
为其前n项和,求 .
.
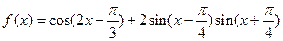
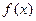 的最小正周期和图象的对称轴方程
的最小正周期和图象的对称轴方程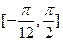 上的值域
上的值域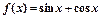 的最小正周期是
的最小正周期是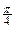

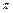
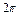
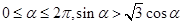 ,则
,则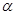 的取值范围是:()
的取值范围是:()



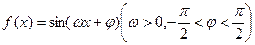 给出下列四个论断:
给出下列四个论断: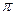 ;
;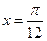 对称;
对称;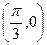 对称;④在区间
对称;④在区间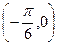 上是增函数。
上是增函数。  的单调增区间为( )
的单调增区间为( )


