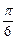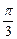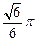题目内容
已知P、A、B、C是球面上四点,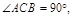
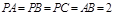 ,则A、B两点间的球面距离是 ( )
,则A、B两点间的球面距离是 ( )
A.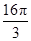 B.
B. 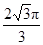
C.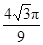 D.
D.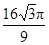
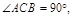
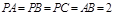 ,则A、B两点间的球面距离是 ( )
,则A、B两点间的球面距离是 ( )A.
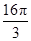 B.
B. 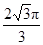
C.
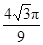 D.
D.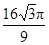
C
本题考查球面距离的求法.
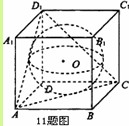
如图示,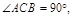 则
则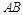 为截面圆
为截面圆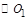 的直径,则
的直径,则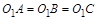 ;又
;又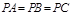 ,则
,则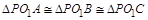 ;于是
;于是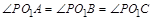
又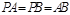 ,则
,则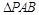 为正三角形,所以
为正三角形,所以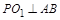 ,即
,即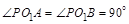 ,所以
,所以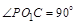 ,即
,即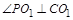 ,则
,则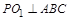 ,所以过球心
,所以过球心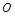 ,故
,故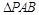 的外接圆即为过
的外接圆即为过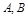 的大圆,从而
的大圆,从而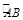 的长即为
的长即为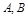 两点间的球面距离。
两点间的球面距离。
因为则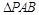 为正三角形,所以
为正三角形,所以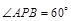 ,所以
,所以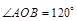 ;
;
又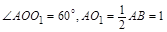 ,则球的半径
,则球的半径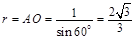 .
.
所以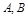 两点间的球面距离为
两点间的球面距离为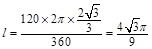
故正确答案为C
如图示,
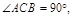 则
则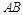 为截面圆
为截面圆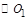 的直径,则
的直径,则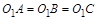 ;又
;又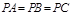 ,则
,则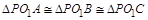 ;于是
;于是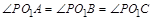
又
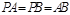 ,则
,则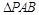 为正三角形,所以
为正三角形,所以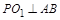 ,即
,即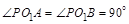 ,所以
,所以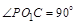 ,即
,即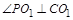 ,则
,则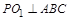 ,所以过球心
,所以过球心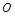 ,故
,故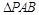 的外接圆即为过
的外接圆即为过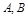 的大圆,从而
的大圆,从而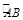 的长即为
的长即为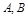 两点间的球面距离。
两点间的球面距离。因为则
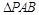 为正三角形,所以
为正三角形,所以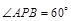 ,所以
,所以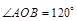 ;
;又
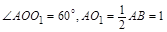 ,则球的半径
,则球的半径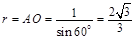 .
.所以
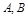 两点间的球面距离为
两点间的球面距离为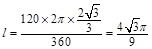
故正确答案为C
 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
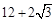



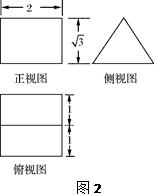
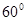 ,则对角线AC1的长是 .
,则对角线AC1的长是 .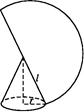
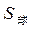 _____
_____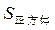 (填”大于、小于或等于”).
(填”大于、小于或等于”).
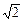 ,四个顶点在同一球面上,则此球的表面积为 .
,四个顶点在同一球面上,则此球的表面积为 .