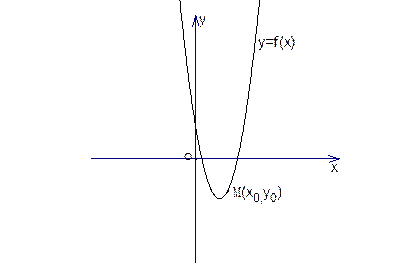题目内容
(本题满分12分)
函数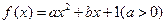
(1)若f(-1)=0,并对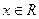 恒有
恒有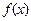
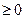 ,求
,求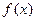 的表达式;
的表达式;
(2)在(1)的条件下,对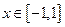 ,
,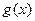 =
=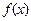 —kx是单调函数,求k的范围。
—kx是单调函数,求k的范围。
函数
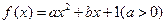
(1)若f(-1)=0,并对
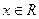 恒有
恒有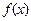
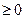 ,求
,求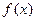 的表达式;
的表达式;(2)在(1)的条件下,对
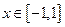 ,
,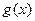 =
=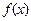 —kx是单调函数,求k的范围。
—kx是单调函数,求k的范围。f(x)=x2+2x+1,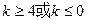
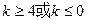
解:(1)由 f(-1)=0得a-b+1=0
又因为对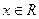 恒有
恒有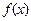
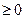 ,⊿=b2-4a≤0,得(a+1)2-4a≤0, (a-1)2≤0,
,⊿=b2-4a≤0,得(a+1)2-4a≤0, (a-1)2≤0,
所以a="1 " b="2 " 得 f(x)=x2+2x+1
(2)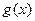 =
=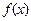 —kx= x2+(2-k)x+1是单调函数,则
—kx= x2+(2-k)x+1是单调函数,则
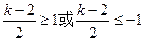 ,所以得
,所以得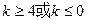
又因为对
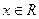 恒有
恒有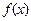
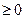 ,⊿=b2-4a≤0,得(a+1)2-4a≤0, (a-1)2≤0,
,⊿=b2-4a≤0,得(a+1)2-4a≤0, (a-1)2≤0,所以a="1 " b="2 " 得 f(x)=x2+2x+1
(2)
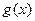 =
=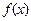 —kx= x2+(2-k)x+1是单调函数,则
—kx= x2+(2-k)x+1是单调函数,则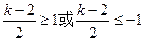 ,所以得
,所以得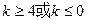

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
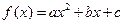 的图象与x轴有两个不同的交点
的图象与x轴有两个不同的交点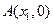 、
、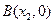 ,且
,且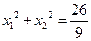 ,试问该二次函数的图象由
,试问该二次函数的图象由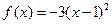 的图象向上平移几个单位得到?
的图象向上平移几个单位得到?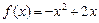 .
. 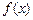 在区间
在区间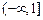 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;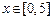 时,求
时,求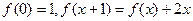
 .
. 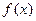 ;
;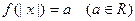 的解的个数.
的解的个数.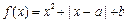 在区间
在区间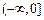 上为减函数,则实数
上为减函数,则实数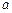 的取值范围是( )
的取值范围是( )



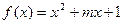 的图像关于直线x=1对称的充要条件是 ( )
的图像关于直线x=1对称的充要条件是 ( )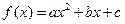 的图象开口向上,且顶点在第二象限,则
的图象开口向上,且顶点在第二象限,则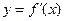 的图象大概是:
的图象大概是: 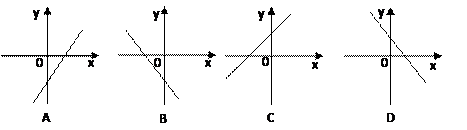
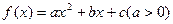 的图像经过点
的图像经过点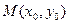 ,且点M在
,且点M在 轴的下方,
轴的下方,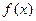 的图像与
的图像与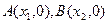 ,求证:
,求证: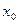 介于
介于 之间。
之间。