题目内容
19.某工厂计划生产A,B两种涂料,生产每吨A中涂料需要甲种原料1t,乙种原料2t,获得利润3千元;上产B种涂料需要甲种原料2t,乙种原料1t,获得利润2千元,又知该工厂甲种原料的用量不超过400t,乙种原料的用量不超过500t,如何安排生产才能获得最大利润?分析 根据已知设出变量设应分别生产A、B两种涂料xt,yt,总利润为Z千元,那么得到x,y的关系式,以及总利润的表达式,进而结合平移法得到最值.
解答 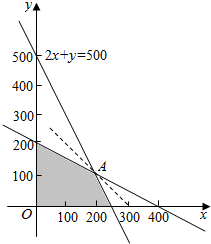 解:设应分别生产A、B两种涂xt,yt,总利润为Z千元…1分
解:设应分别生产A、B两种涂xt,yt,总利润为Z千元…1分
则线性约束条件是$\left\{\begin{array}{l}{x≥0,y≥0}\\{x+2y≤400}\\{2x+y≤500}\end{array}\right.$
目标函数z=3x+2y,…6分
作出可行域,如图所示:…8分
平移可知,当直线$y=-\frac{3}{2}x+\frac{z}{2}$,
经过点A时,纵截距最大,则z取得最大值.
由$\left\{\begin{array}{l}{2x+y=500}\\{x+2y=400}\end{array}\right.$ 得$\left\{\begin{array}{l}{x=200}\\{y=100}\end{array}\right.$,
即A(200,100)
此时z=3×200+2×100=800千元.…11分
答:应分别生产A、B两种涂料各200t、100t才能获得最大利润.…12分
点评 本题主要考查线性规划的最优解问题在实际生活中的运用.设出变量,建立约束条件,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
10.“|x-2|>3”是“x>5”的( )
| A. | 必要而不充分条件 | B. | 充分而不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.终边在y轴上的角构成的集合可以表示为( )
| A. | {α|α=$\frac{π}{2}$+2kπ,k∈Z} | B. | {α|α=$\frac{3π}{2}$+2kπ,k∈Z} | C. | {α|α=$\frac{kπ}{2}$,k∈Z} | D. | {α|α=$\frac{π}{2}$+kπ,k∈Z} |
8.正态总体N(0,1)中,数值落在(-∞,-3)∪(3,+∞)内的概率是( )
| A. | 4.6% | B. | 0.002 | C. | 0.003 | D. | 3% |