题目内容
【题目】如图，设锐角
的外接圆的半径为
，在内取外接圆的同心圆
，其半径为
，从圆上任取一点
，作
于点
，
于点
，
于点
．
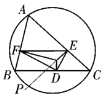
（1）求证：
的面积为定值；
（2）猜想：当为任意三角形、同心圆为任意同心圆时，结论是否成立（不要求证明）？
【答案】（1）见解析；（2）见解析
【解析】
（1）如图，联结
交外接圆于点
，联结
交外接圆于点
，过
作直径
．
由相交弦定理有
． ①
又由
，
，知、
、
、
四点共圆．则
②
③
同理，由
，，有
， ④
． ⑤
由、
、
、四点共圆知
， ⑥
． ⑦
由式③、⑤、⑥有
． ⑧
把式⑦、⑧代入
，由正弦定理得
． ⑨
把①、②、④、⑨代入
的面积公式有
（定值）．
（2）当
为任意三角形、同心圆
为任意同心圆时，结论成立．证明是类似的．当点在外接圆上时，面积为零，得三点共线（西姆松线）．
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
【题目】从某企业生产的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量表得如下频数分布表：
质量指标值分组 | [75，85) | [85，95) | [95，105) | [105，115) | [115，125) |
频数 | 6 | 26 | 38 | 22 | 8 |
（I）在答题卡上作出这些数据的频率分布直方图：
（II）估计这种产品质量指标值的平均数及方差（同一组中的数据用该组区间的中点值作代表）；
（III）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定？
【题目】已知某公司成本为
元，所得的利润
元的几组数据入下.
第一组 | 第二组 | 第三组 | 第四组 | 第五组 | |
| 1 | 4 | 5 | 2 | 3 |
| 2 | 1 | 3 | 4 | 0 |
根据上表数据求得回归直线方程为：
（1）若这个公司所规划的利润为200万元，估算一下它的成本可能是多少？（保留1位小数）
（2）在每一组数据中，，相差
，记为事件
；，相差
，记为事件
；，相差
，记为事件
.随机抽两组进行分析，则抽到有事件发生的概率.
