Question

【题目】已知函数.

（1）求曲线y=f（x）在点处的切线与坐标轴围成的三角形的面积；

（2）求过点作曲线y=f（x）的切线方程.

Answer 1

【答案】（1）；（2）y或18x﹣2y﹣35=0.

【解析】

（1）函数的导数为=x2，曲线y=f（x）在点处的切线的斜率为k=1，写出切线的方程，分别令x=0，y=0，得到在x，y轴上的截距，再利用三角形面积公式求解.

（2）易得A（2，）不在图象上，设切点为（m，n），则切线的斜率为m2，切线的方程为y﹣n=m2（x﹣m），再由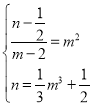求解.

（1）因为函数，

所以=x2，

所以

所以曲线y=f（x）在点处的切线的斜率为k=1，

则切线的方程为yx﹣1，即为6x﹣6y﹣1=0，

令x=0，可得y；y=0，可得x.

则切线与坐标轴围成的三角形的面积为S；

（2）由A（2，）和，可得f（2），

即A不在f（x）的图象上，

设切点为（m，n），则切线的斜率为m2，

切线的方程为y﹣n=m2（x﹣m），

则，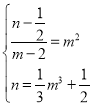

解得或，

故切线的方程为y或18x﹣2y﹣35=0.