题目内容
数列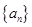 的前
的前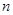 项和为
项和为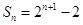 ,数列
,数列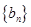 是首项为
是首项为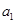 ,公差为
,公差为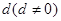 的等差数列,且
的等差数列,且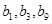 成等比数列.
成等比数列.
(Ⅰ)求数列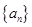 与
与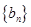 的通项公式;
的通项公式;
(Ⅱ)若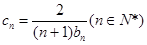 ,求数列
,求数列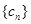 的前
的前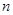 项和
项和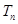 .
.
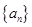 的前
的前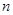 项和为
项和为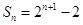 ,数列
,数列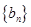 是首项为
是首项为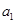 ,公差为
,公差为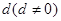 的等差数列,且
的等差数列,且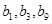 成等比数列.
成等比数列.(Ⅰ)求数列
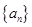 与
与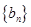 的通项公式;
的通项公式;(Ⅱ)若
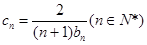 ,求数列
,求数列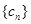 的前
的前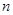 项和
项和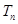 .
.(Ⅰ) ;(Ⅱ)
;(Ⅱ)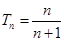 .
.
 ;(Ⅱ)
;(Ⅱ)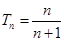 .
.试题分析:(Ⅰ)通过讨论
 时,
时, ,验证
,验证 ,是否满足上式,确定得到数列{
,是否满足上式,确定得到数列{ }的通项公式.进一步应用等比数列知识,建立公差的方程,确定得到
}的通项公式.进一步应用等比数列知识,建立公差的方程,确定得到 .(Ⅱ)针对
.(Ⅱ)针对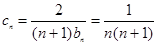 利用“裂项相消法”求得
利用“裂项相消法”求得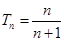 .
.试题解析:(Ⅰ)当
 ,时
,时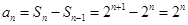 , 2分
, 2分又
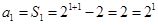 ,也满足上式,
,也满足上式,所以数列{
 }的通项公式为
}的通项公式为 . 3分
. 3分 ,设公差为
,设公差为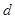 ,则由
,则由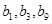 成等比数列,
成等比数列,得
 , 4分
, 4分解得
 (舍去)或
(舍去)或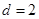 , 5分
, 5分所以数列
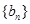 的通项公式为
的通项公式为 . 6分
. 6分(Ⅱ)解:
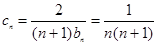 8分
8分数列
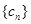 的前
的前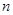 项和
项和

 10分
10分 . 12分
. 12分
练习册系列答案
相关题目
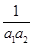 +
+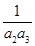 +…+
+…+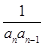 <
<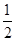 .
.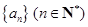 的前
的前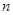 项和为
项和为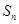 ,且
,且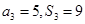 .
.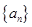 的通项公式;
的通项公式;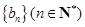 ,若
,若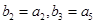 ,求数列
,求数列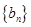 的前
的前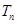 .
.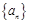 是首项为1,公差为
是首项为1,公差为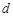 的等差数列,数列
的等差数列,数列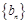 是首项为1,公比为
是首项为1,公比为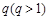 的等比
的等比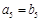 ,
,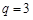 ,求数列
,求数列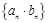 的前
的前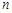 项和;
项和;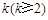 ,使得
,使得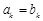 .试比较
.试比较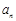 与
与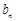 的大小,并说明理由.
的大小,并说明理由.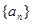 中
中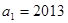 ,前
,前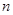 项和为
项和为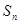 ,
,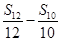
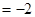 ,则
,则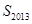 的值为__________.
的值为__________.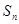 为等差数列
为等差数列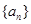 的前n项和,
的前n项和,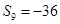 ,
,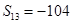 ,则
,则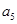 与
与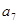 的等比中项为( )
的等比中项为( )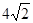 B.
B.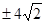 C.4 D.
C.4 D.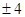
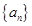 满足
满足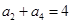 ,
,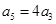 ,则数列
,则数列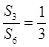 ,则
,则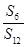 =
=  为等差数列
为等差数列 的前n项和,若
的前n项和,若 ,则
,则 = .
= .