题目内容
(本题满分12分)
已知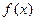 是定义在
是定义在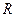 上的函数,且满足下列条件:
上的函数,且满足下列条件:
①对任意的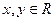 ,
,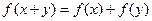 ;②当
;②当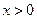 时,
时,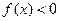 .
.
(1)证明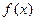 是定义在
是定义在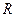 上的减函数;
上的减函数;
(2)如果对任意实数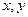 ,有
,有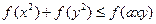 恒成立,求实数
恒成立,求实数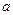 的取值范围。
的取值范围。
已知
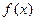 是定义在
是定义在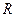 上的函数,且满足下列条件:
上的函数,且满足下列条件:①对任意的
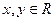 ,
,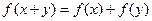 ;②当
;②当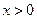 时,
时,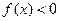 .
.(1)证明
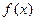 是定义在
是定义在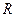 上的减函数;
上的减函数;(2)如果对任意实数
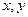 ,有
,有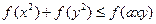 恒成立,求实数
恒成立,求实数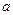 的取值范围。
的取值范围。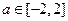
解:(1)令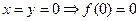 ,所以
,所以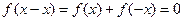 ,所以
,所以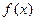 是寄函数,在R上任意取
是寄函数,在R上任意取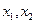 ,且
,且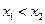 ,
,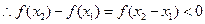
所以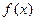 是定义在
是定义在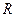 上是减函数;………….6分
上是减函数;………….6分
(2)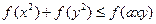 恒成立,即
恒成立,即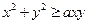 ,
,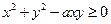 对x恒成立,
对x恒成立,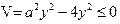 恒成立,对任意y恒成立,即
恒成立,对任意y恒成立,即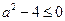 ,即
,即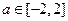 。………12分
。………12分
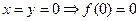 ,所以
,所以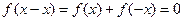 ,所以
,所以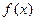 是寄函数,在R上任意取
是寄函数,在R上任意取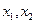 ,且
,且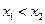 ,
,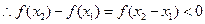
所以
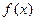 是定义在
是定义在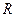 上是减函数;………….6分
上是减函数;………….6分(2)
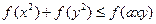 恒成立,即
恒成立,即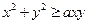 ,
,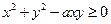 对x恒成立,
对x恒成立,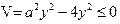 恒成立,对任意y恒成立,即
恒成立,对任意y恒成立,即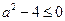 ,即
,即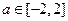 。………12分
。………12分
练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
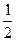 )x的图像关于直线y=x对称,则
)x的图像关于直线y=x对称,则 的单调递增区间( )
的单调递增区间( )

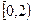

 (1)当a=4,
(1)当a=4,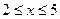 ,求函数f(x)的最大值;(2)若x≥a , 试求f(x)+3 >0 的解集;(3)当
,求函数f(x)的最大值;(2)若x≥a , 试求f(x)+3 >0 的解集;(3)当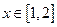 时,f(x)≤2x – 2 恒成立,求实数a的取值范围.
时,f(x)≤2x – 2 恒成立,求实数a的取值范围.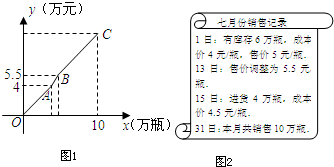
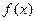 是奇函数,且在(
是奇函数,且在(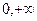 ),内是增函数,
),内是增函数, ,则不等式
,则不等式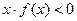 的解集为 ( )
的解集为 ( )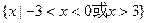
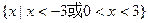
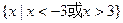
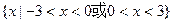
 的最大值是 。
的最大值是 。