题目内容
已知函数f(x)=
,若f(x)在(-∞,+∞)上单调递增,则实数a的取值范围为______.
|
由于函数f(x)=
,f(x)在(-∞,+∞)上单调递增,
故有 a-1>0,且loga1≥(a-1)-1,即 0≥a-2.
综合可得 1<a≤2,
故答案为 (1,2].
|
故有 a-1>0,且loga1≥(a-1)-1,即 0≥a-2.
综合可得 1<a≤2,
故答案为 (1,2].

练习册系列答案
相关题目
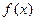 是定义在
是定义在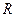 上的函数,且满足下列条件:
上的函数,且满足下列条件: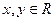 ,
,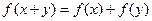 ;②当
;②当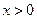 时,
时,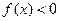 .
.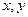 ,有
,有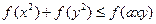 恒成立,求实数
恒成立,求实数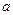 的取值范围。
的取值范围。