题目内容
已知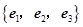 为空间的一个基底,且
为空间的一个基底,且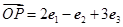 ,
, 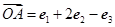 ,
,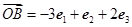 ,
,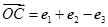
(1)判断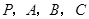 四点是否共面;
四点是否共面;
(2)能否以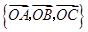 作为空间的一个基底?若不能,说明理由;若能,试以这一基底表示向量
作为空间的一个基底?若不能,说明理由;若能,试以这一基底表示向量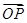
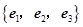 为空间的一个基底,且
为空间的一个基底,且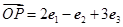 ,
, 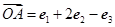 ,
,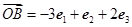 ,
,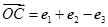
(1)判断
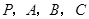 四点是否共面;
四点是否共面;(2)能否以
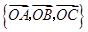 作为空间的一个基底?若不能,说明理由;若能,试以这一基底表示向量
作为空间的一个基底?若不能,说明理由;若能,试以这一基底表示向量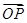
(1)四点不共面; (2)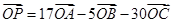 .
.
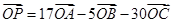 .
.本试题主要是考查了空间向量中四点共面的问题,以及判定空间向量的基底的定义的运用。
(1)假设四点共面,则存在实数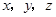 使
使 ,
,
且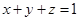 ,那么可以根据这个结论得到方程组,求解判定不成立。
,那么可以根据这个结论得到方程组,求解判定不成立。
(2)利用不同面的三个向量可以充当空间的基底,那么我们可以得到,判定
解:(1)假设四点共面,则存在实数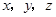 使
使 ,
,
且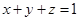 ,
,
即 .…4分
.…4分
比较对应的系数,得一关于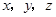 的方程组
的方程组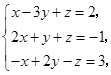
解得
与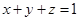 矛盾,故四点不共面;……………6分
矛盾,故四点不共面;……………6分
(2)若向量 ,
, ,
, 共面,则存在实数
共面,则存在实数 使
使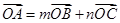 ,
,
同(1)可证,这不可能,
因此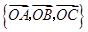 可以作为空间的一个基底,
可以作为空间的一个基底,
令 ,
,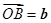 ,
,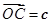 ,
,
由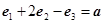 ,
, ,
,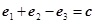 联立得到方程组,
联立得到方程组,
从中解得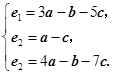 ………………10分所以
………………10分所以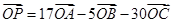
(1)假设四点共面,则存在实数
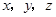 使
使 ,
,且
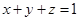 ,那么可以根据这个结论得到方程组,求解判定不成立。
,那么可以根据这个结论得到方程组,求解判定不成立。(2)利用不同面的三个向量可以充当空间的基底,那么我们可以得到,判定
解:(1)假设四点共面,则存在实数
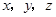 使
使 ,
,且
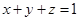 ,
,即
 .…4分
.…4分比较对应的系数,得一关于
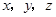 的方程组
的方程组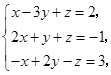
解得

与
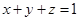 矛盾,故四点不共面;……………6分
矛盾,故四点不共面;……………6分(2)若向量
 ,
, ,
, 共面,则存在实数
共面,则存在实数 使
使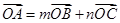 ,
,同(1)可证,这不可能,
因此
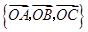 可以作为空间的一个基底,
可以作为空间的一个基底,令
 ,
,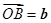 ,
,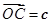 ,
,由
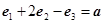 ,
, ,
,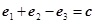 联立得到方程组,
联立得到方程组,从中解得
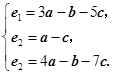 ………………10分所以
………………10分所以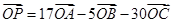

练习册系列答案
相关题目
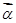 、
、 、
、 满足
满足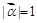 ,
,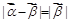 ,
, .若对每一确定的
.若对每一确定的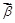 ,
, 的最大值和最小值分别为
的最大值和最小值分别为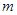 、
、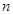 ,则对任意
,则对任意 的最小值是 ( )
的最小值是 ( )
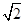
 为正方形,
为正方形,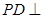 平面
平面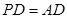 ,则
,则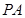 与
与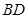 所成角的度数为
所成角的度数为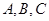 是圆
是圆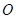 上的三点,
上的三点,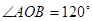 ,
,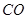 的延长线与线段
的延长线与线段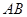 交于点
交于点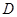 ,若
,若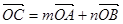
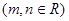 ,则
,则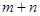 的取值范围是
的取值范围是 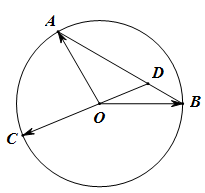 .
.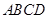 的边长为
的边长为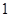 ,点
,点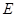 在边
在边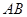 上,点
上,点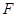 在边
在边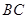 上,
上,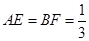 。动点
。动点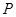 从
从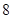


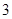
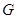 为△
为△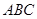 的重心,且
的重心,且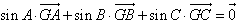 ,则
,则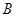 的大小为( )
的大小为( )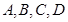 是平面
是平面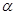 内的四个定点,平面
内的四个定点,平面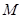 满足
满足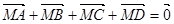 这样的点
这样的点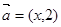 ,
,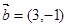 ,若(
,若(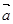 +
+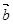 )//(
)//(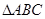 中,
中,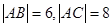 ,
,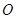 为
为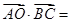 ________.
________.