题目内容
若称 为n个正数a1+a2+…+an的“均倒数”已知数列{an}的各项均为正,且其前n项的“均倒数”为
为n个正数a1+a2+…+an的“均倒数”已知数列{an}的各项均为正,且其前n项的“均倒数”为 则数列{an}的通项公式为
则数列{an}的通项公式为
 为n个正数a1+a2+…+an的“均倒数”已知数列{an}的各项均为正,且其前n项的“均倒数”为
为n个正数a1+a2+…+an的“均倒数”已知数列{an}的各项均为正,且其前n项的“均倒数”为 则数列{an}的通项公式为
则数列{an}的通项公式为A. | B. | C. | D. |
B
试题分析:由题意可知前n项和
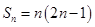 ,当
,当 时
时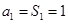 ,当
,当 时
时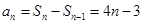 ,经验证
,经验证 符合,所以通项为
符合,所以通项为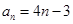
点评:由数列前n项和
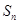 求通项
求通项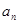 时主要利用
时主要利用 分别求出后验证最终结果能否合并
分别求出后验证最终结果能否合并
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 满足
满足 ,
, ,
, ,则
,则 项和
项和 = .
= . 的前
的前 项和
项和 ,第
,第 项满足
项满足 ,则k=( )
,则k=( ) 的前
的前 项和为
项和为 ,
, ,
, ,,则
,,则 ( )
( )



 的通项公式
的通项公式 ,其前
,其前 项和为
项和为 ,则
,则 等于( )
等于( ) 中,
中, ,
, ,则当
,则当 取得最小值时
取得最小值时 的值是 .
的值是 . 的通项公式
的通项公式 ,其前
,其前 项和为
项和为 ,则
,则 等于( A )
等于( A )



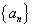 ,首项a 1 =3且2a n+1="S" n?S n-1 (n≥2).
,首项a 1 =3且2a n+1="S" n?S n-1 (n≥2).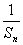 }是等差数列,并求公差;
}是等差数列,并求公差;