题目内容
设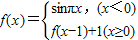 ,
,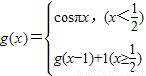 ,则
,则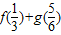 = .
= .
【答案】分析:分段函数的求值问题,必须分段考虑,由于  >0,
>0,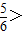
 ,故利用下面一个式子求解.
,故利用下面一个式子求解.
解答:解:因为 >0,
>0,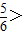
 ,
,
所以:f( )=f(
)=f( -1)+1=f(-
-1)+1=f(- )+1=sin(-
)+1=sin(-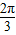 )+1=1-
)+1=1-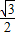 .
.
g( )=g(
)=g( -1)+1=g(-
-1)+1=g(- )+1=cos(-
)+1=cos(-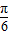 )+1=
)+1=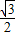 +1.
+1.
∴f( )+g(
)+g( )=2.
)=2.
故答案为2.
点评:本题考查了分段函数的定义,求分段函数函数值的方法,解题时要认真细致,准确运算.分段函数是指在定义域的不同阶段上对应法则不同,因此分段函数求函数值时,一定要看清楚自变量所处阶段.
 >0,
>0,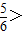
 ,故利用下面一个式子求解.
,故利用下面一个式子求解.解答:解:因为
 >0,
>0,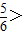
 ,
,所以:f(
 )=f(
)=f( -1)+1=f(-
-1)+1=f(- )+1=sin(-
)+1=sin(-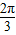 )+1=1-
)+1=1-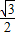 .
.g(
 )=g(
)=g( -1)+1=g(-
-1)+1=g(- )+1=cos(-
)+1=cos(-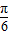 )+1=
)+1=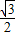 +1.
+1.∴f(
 )+g(
)+g( )=2.
)=2.故答案为2.
点评:本题考查了分段函数的定义,求分段函数函数值的方法,解题时要认真细致,准确运算.分段函数是指在定义域的不同阶段上对应法则不同,因此分段函数求函数值时,一定要看清楚自变量所处阶段.

练习册系列答案
相关题目
 已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的左边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设∠MNB=θ,则θ的取值范围为
已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的左边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设∠MNB=θ,则θ的取值范围为