题目内容
设α∈R,则“a=1”是“f(x)=lg(a+
)为奇函数”的( )
| 2 |
| x-1 |
分析:首先明白函数f(x)是奇函数必须满足:定义域关于原点对称及定义域内的任意x满足f(-x)+f(x)=0.再验证是否满足充要条件即可.
解答:解:“?”:a=1时,f(x)=lg
,由
>0,解得x<-1或x>1,∴函数f(x)的定义域为(-∞,-1)∪(1,+∞)关于原点对称;
又f(-x)+f(x)=lg
+lg
=lg1=0,∴函数f(x)是奇函数.
“?”:若f(x)=lg(a+
)为奇函数,则f(-x)+f(x)=lg(a+
)+lg(a+
)=0,
化为(a-1)[(a+1)(x2-1)+4]=0,此式对于定义域内的任意x皆成立,必有a=1,由上面可知a=1满足题意.
故“a=1”是“f(x)=lg(a+
)为奇函数”的充要条件.
故选C.
| x+1 |
| x-1 |
| x+1 |
| x-1 |
又f(-x)+f(x)=lg
| -x+1 |
| -x-1 |
| x+1 |
| x-1 |
“?”:若f(x)=lg(a+
| 2 |
| x-1 |
| 2 |
| x-1 |
| 2 |
| -x-1 |
化为(a-1)[(a+1)(x2-1)+4]=0,此式对于定义域内的任意x皆成立,必有a=1,由上面可知a=1满足题意.
故“a=1”是“f(x)=lg(a+
| 2 |
| x-1 |
故选C.
点评:充分理解奇函数的定义和充要条件是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 )为奇函数”的
)为奇函数”的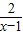 )为奇函数”的( )
)为奇函数”的( )