题目内容
已知矩形纸片ABCD中，AB=6cm，AD=12cm，将矩形纸片的右下角折起，使得该角的顶点B落在矩形的左边AD上，且折痕MN的两端点M、N分别位于边AB、BC上，设∠MNB=θ，则θ的取值范围为[
，
]
| π |
| 12 |
| π |
| 4 |
[
，
]
．| π |
| 12 |
| π |
| 4 |
分析：将矩形纸片的右下角折起，使该角的顶点B落在矩形的边AD上，则△MNE≌△MNB，EM=BM，由∠MNB=θ，MN=l．由AB=6cm，可得EM+AM=6，然后将EM与BM分别用含θ的式子表示，即可求出θ的范围．
解答：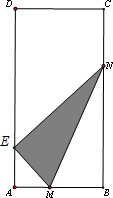
解：如图所示，∠AEM=90°-2θ，
则MB=lsinθ，AM=l•sinθsin（90°-θ），
由题设得：lsinθ+l•sinθsin（90°-2θ）=6，
从而得l=
，
即：l=
，l=
由
得
，
解得：
≤θ≤
，
故答案为：[
，
]．
解：如图所示，∠AEM=90°-2θ，则MB=lsinθ，AM=l•sinθsin（90°-θ），
由题设得：lsinθ+l•sinθsin（90°-2θ）=6，
从而得l=
| 6 |
| sinθ+sinθsin(90°-2θ) |
即：l=
| 6 |
| sinθ+sinθcos2θ |
| 3 |
| sinθ•cos2θ |
由
|
得
|
解得：
| π |
| 12 |
| π |
| 4 |
故答案为：[
| π |
| 12 |
| π |
| 4 |
点评：在求实际问题对应的函数的解析式，要进一步分析自变量的取值范围，这不仅是为了让函数的解析式更准确，而且为利用函数的解析式求函数的值域，最值、单调性、奇偶性等打好基础．
练习册系列答案
阅读快车系列答案
相关题目
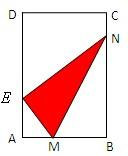已知矩形纸片ABCD中，AB=6cm，AD=12cm，将矩形纸片的右下角折起，使该角的顶点B落在矩形的边AD上，且折痕MN的两端点M、N分别位于边AB、BC上，设∠MNB=θ，MN=l．
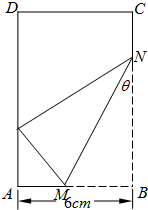已知矩形纸片ABCD中，AB=6cm，AD=12cm，将矩形纸片的右下角折起，使得该角的顶点B落在矩形的边AD上，且折痕MN的端点M，N分别位于边AB，BC上，设∠MNB=θ，sinθ=t，MN长度为l．
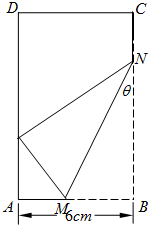已知矩形纸片ABCD中，AB=6cm，AD=12cm，将矩形纸片的右下角折起，使得该角的顶点B落在矩形的边AD上，且折痕MN的端点M，N分别位于边AB，BC上，设∠MNB=θ，sinθ=t，MN长度为l．
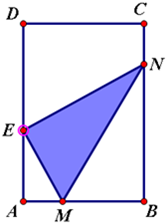已知矩形纸片ABCD中，AB=6，AD=12，将举行制品的右下角沿线段MN折叠，使矩形的顶点B落在矩形的边AD上，记该点为E，且折痕MN的两端点M、N分别位于边AB，BC上，设∠MNB=θ，MN=l，△EMN的面积为S，