题目内容
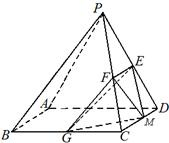 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.(I)求证:PA∥平面EFG;
(II)求平面EFG⊥平面PAD;
(III)若M是线段CD上一点,求三棱锥M-EFG的体积.
分析:(I)取AD的中点H,连接EH,HG,可以证明E,F,G,H四点共面,再利用直线与平面平行的判定定理进行证明,即可解决问题;
(II)由题意AD⊥CD,PD⊥CD,可得CD⊥平面PAD,因为EF∥CD,证明EF⊥平面PAD,从而求解.
(III)CD∥EF,所以CD∥平面EFG,故CD上的点M到平面EFG的距离等于D到平面EFG的距离,利用公式VM-EFG=VD-EFG,进行求解.
(II)由题意AD⊥CD,PD⊥CD,可得CD⊥平面PAD,因为EF∥CD,证明EF⊥平面PAD,从而求解.
(III)CD∥EF,所以CD∥平面EFG,故CD上的点M到平面EFG的距离等于D到平面EFG的距离,利用公式VM-EFG=VD-EFG,进行求解.
解答: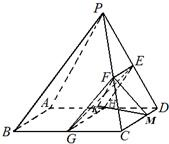 解:(I)证明:取AD的中点H,连接EH,HG.
解:(I)证明:取AD的中点H,连接EH,HG.
∵H,G为AD,BC的中点,∴HG∥CD,
又EF∥CD.∴EF∥HG,
∴E,F,G,H四点共面,(2分)
又∵PA∥EH,EH?平面EFGH,PA?平面EFGH,
∴PA∥平面EFG.(4分)
(II)证明:∵AD⊥CD,PD⊥CD,
∴CD⊥平面PAD,(6分)
∵EF∥CD,∴EF⊥平面PAD,
∵EF?平面EFG,∴平面EFG⊥平面PAD;(8分)
(III)解:∵CD∥EF,∴CD∥平面EFG,
故CD上的点M到平面EFG的距离
等于D到平面EFG的距离,∴VM-EFG=VD-EFG,(10分)
S△EFG=
×EF×EH=2,平面EFGH⊥平面PBD于EH,
∴D到平面EFG的距离即三角形EHD的高,等于
∴VM-EFG=
.(12分)
 解:(I)证明:取AD的中点H,连接EH,HG.
解:(I)证明:取AD的中点H,连接EH,HG.∵H,G为AD,BC的中点,∴HG∥CD,
又EF∥CD.∴EF∥HG,
∴E,F,G,H四点共面,(2分)
又∵PA∥EH,EH?平面EFGH,PA?平面EFGH,
∴PA∥平面EFG.(4分)
(II)证明:∵AD⊥CD,PD⊥CD,
∴CD⊥平面PAD,(6分)
∵EF∥CD,∴EF⊥平面PAD,
∵EF?平面EFG,∴平面EFG⊥平面PAD;(8分)
(III)解:∵CD∥EF,∴CD∥平面EFG,
故CD上的点M到平面EFG的距离
等于D到平面EFG的距离,∴VM-EFG=VD-EFG,(10分)
S△EFG=
| 1 |
| 2 |
∴D到平面EFG的距离即三角形EHD的高,等于
| 3 |
∴VM-EFG=
2
| ||
| 3 |
点评:此题考查直线与平面平行的判断及平面与平面垂直的判断,此类问题一般先证明两个面平行,再证直线和面平行,这种做题思想要记住,此类立体几何题是每年高考必考的一道大题,同学们要课下要多练习.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
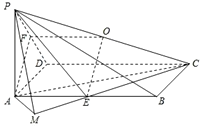 已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点. (2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点.
(2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点. (2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点.
(2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点. 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ< (2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.