题目内容
【题目】函数f(x)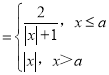 ,若任意t∈(a﹣1,a),使得f(t)>f(t+1),则实数a的取值范围为______.
,若任意t∈(a﹣1,a),使得f(t)>f(t+1),则实数a的取值范围为______.
【答案】1![]() a
a![]() 1
1
【解析】
根据f(x)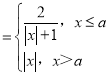 ,由t∈(a﹣1,a)t+1∈(a,a+1),得到f(t)
,由t∈(a﹣1,a)t+1∈(a,a+1),得到f(t)![]() ;f(t+1)=|t+1|;再根据任意t∈(a﹣1,a),使得f(t)>f(t+1),即
;f(t+1)=|t+1|;再根据任意t∈(a﹣1,a),使得f(t)>f(t+1),即![]() |t+1||t+1|(|t|+1)﹣2<0;然后分当t>0,﹣1≤t≤0,t<﹣1时,解不等式得
|t+1||t+1|(|t|+1)﹣2<0;然后分当t>0,﹣1≤t≤0,t<﹣1时,解不等式得![]() t
t![]() 1;根据若任意t∈(a﹣1,a),使得f(t)>f(t+1)成立,则(a﹣1,a)是(
1;根据若任意t∈(a﹣1,a),使得f(t)>f(t+1)成立,则(a﹣1,a)是(![]()
![]() 1)的子集求解.
1)的子集求解.
因为:f(x)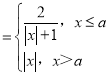 ,
,
由t∈(a﹣1,a)t+1∈(a,a+1),
∴f(t)![]() ;f(t+1)=|t+1|;
;f(t+1)=|t+1|;
∵任意t∈(a﹣1,a),使得f(t)>f(t+1),
∴![]() |t+1|
|t+1|![]() ;①
;①
当t>0时,①式转化为![]() 0<t
0<t![]() ;
;
当![]() 时①式转化为
时①式转化为![]()
![]() ,∴
,∴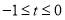 ;
;
t<﹣1时①式转化为![]() t2﹣3<0
t2﹣3<0![]() t<0;
t<0;
综上可得![]() t
t![]() 1;
1;
∵若任意t∈(a﹣1,a),使得f(t)>f(t+1),
∴a﹣1![]() 且a
且a![]() 1;
1;
∴1![]() a
a![]() 1;
1;

练习册系列答案
相关题目