题目内容
(本小题满分14分)
已知二次函数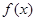 满足以下两个条件:
满足以下两个条件:
①不等式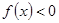 的解集是(-2,0) ②函数
的解集是(-2,0) ②函数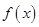 在
在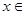
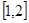 上的最小值是3
上的最小值是3
(Ⅰ)求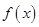 的解析式;
的解析式;
(Ⅱ)若点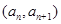
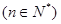 在函数
在函数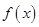 的图象上,且
的图象上,且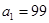
(ⅰ)求证:数列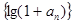 为等比数列
为等比数列
(ⅱ)令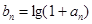 ,是否存在正实数
,是否存在正实数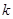 ,使不等式
,使不等式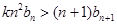 对于一切的
对于一切的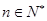 恒成立?若存在,指出
恒成立?若存在,指出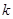 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(Ⅰ)f(x)= x 2 + 2 x .
(Ⅱ)(ⅰ)见解析;(ⅱ)
【解析】
试题分析:(Ⅰ)因为根据题意可知f(x)< 0 的解集为(-2,0),且f(x)是二次函数
因此可设 f(x)= a x(x + 2)
(a > 0),故 f(x)的对称轴为直线  ,
,
f(x)在 [1,2]上的最小值为f(1)=3a =3 ,得到参数a的值。
(Ⅱ)(ⅰ)因为点(a n , a n + 1 )在函数f(x)= x 2 + 2 x 的图象上
∴得到递推关系式 a n + 1 = a n 2 + 2 a n , 构造等比数列求解通项公式。
(ⅱ)由上题可知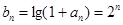 ,要使得不等式
,要使得不等式 恒成立,即
恒成立,即 对于一切的
对于一切的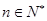 恒成立,转换为二次不等式求解。
恒成立,转换为二次不等式求解。
解:(Ⅰ)∵ f(x)< 0 的解集为(-2,0),且f(x)是二次函数
∴ 可设
f(x)= a x(x + 2) (a > 0),故
f(x)的对称轴为直线  ,
,
∴ f(x)在 [1,2]上的最小值为f(1)=3a =3 ,
∴ a = 1 ,所以f(x)= x 2 + 2 x .
(Ⅱ)(ⅰ)∵ 点(a n , a n + 1 )在函数f(x)= x 2 + 2 x 的图象上,
∴ a n + 1 = a n 2 + 2 a n ,则 1 + a n + 1 = 1 + a n 2 + 2 a n = (1 + a n)2
∴ 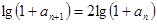 , 又首项
, 又首项 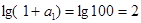
∴ 数列 为等比数列,且公比为2 。
为等比数列,且公比为2 。
(ⅱ)由上题可知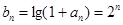 ,要使得不等式
,要使得不等式 恒成立,即
恒成立,即 对于一切的
对于一切的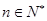 恒成立,
恒成立,
法一: 对一切的
对一切的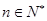 恒成立,
恒成立,
令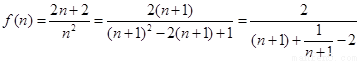 ,
,
∵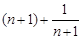 在
在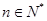 是单调递增的,∴
是单调递增的,∴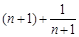 的最小值为
的最小值为
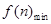 =
= 所以
所以
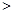
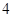
法二:
设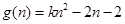
当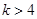 时,由于对称轴直线
时,由于对称轴直线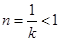 ,且
,且 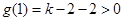 ,而函数
,而函数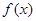 在
在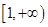 是增函数,∴不等式
是增函数,∴不等式 恒成立
恒成立
即当
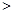
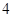 时,不等式
时,不等式 对于一切的
对于一切的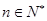 恒成立
恒成立
考点:本试题主要考查了数列、不等式知识,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.
点评:解题时要注意对于不等式恒成立问题的等价转化为一元二次不等式问题。

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)